第 8 章 生成模型

目前越来越多的基于生成式的软件出现，极大程度上改变了我们的生活。例如，我们可以通过一张照片，让软件自动生成一段音乐，或者是让软件自动生成一段视频。本章具体介绍它们背后的基础模型——生成模型。

8.1 生成对抗网络

本章介绍生成模型（generative model）。到目前为止，我们学习到的网络本质上都是一个函数，即提供一个输入 $x$ ，网络就可以输出一个结果 $y$ 。并且我们在前几章已经了解各种各样的网络，它们可以应对不同类型的输入 $x$ 和输出 $y$ 。例如，当输入 $x$ 是一张图片时，可以使用例如卷积神经网络等模型进行处理，当输入 $x$ 是序列数据时，可以使用基于循环神经网络架构的模型进行处理，其中输出 $y$ 既可以是数值、类别，也可以是一个序列。目前，这些网络已经可以涵盖多数我们日常会遇到的问题了。

8.1.1 生成器

接下来，我们将介绍另一种架构— 生成模型。与先前介绍的模型不同的是，生成模型中网络会被作为一个生成器（generator）来使用。具体来说，在模型输入时会将一个随机变量 $z$ 与原始输入 $x$ 一并输入到模型中，这个变量是从随机分布中采样得到。输入时可以采用向量拼接的方式将 $x$ 和 $z$ 一并输入，或在 $x$ 、 $z$ 长度一样时，将二者的加和作为输入。这个变量 $z$ 特别之处在于其非固定性，即每一次我们使用网络时都会从一个随机分布中采样得到一个新的 $z$ 。通常，我们对于该随机分布的要求是其足够简单，可以较为容易地进行采样，或者可以直接写出该随机分布的函数，例如高斯分布（Gaussian distribution）、均匀分布（uniform distribution）等等。所以每次有一个输入 $x$ 的同时，我们都从随机分布中采样得到 $z$ ，来得到最终的输出 $y$ 。随着采样得到的 $z$ 的不同，我们得到的输出 $y$ 也会不一样。同理，对于网络来说，其输出也不再固定，而变成了一个复杂的分布，我们也将这种可以输出一个复杂分布的网络称为生成器，如图 8.1 所示。

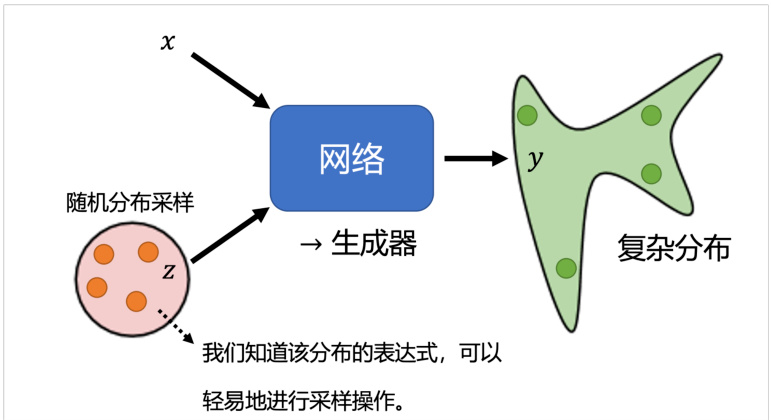
图 8.1 生成器示意图

下面我们介绍如何训练这个生成器。首先，我们为什么要需要训练生成器，为什么需要输出一个分布呢？下面介绍一个视频预测的例子，即给模型一段的视频短片，然后让它预测接下来发生的事情。视频环境是小精灵游戏，预测下一帧的游戏画面，如图 8.2 所示。

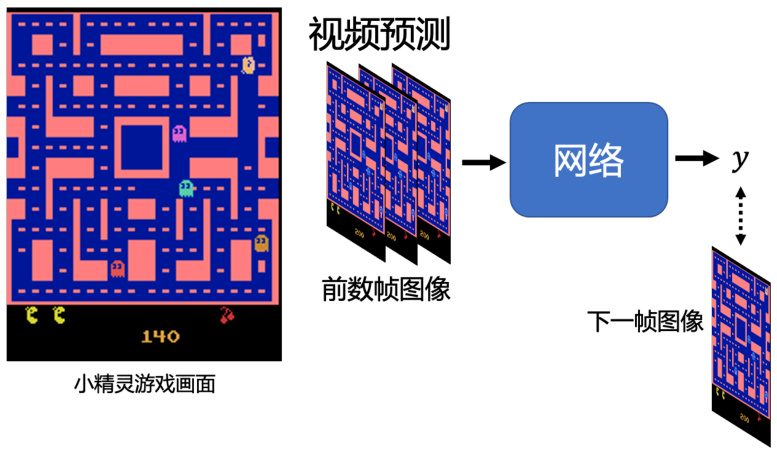
图 8.2 视频预测例子— 以小精灵游戏为例

要预测下一帧的游戏画面，我们只需要输入给网络过去几帧游戏画面。要得到这样的训练数据很简单，只需要在玩小精灵的同时进行录制，就可以训练我们的网络，只要让网络的输出 $y$ ，与我们的真实图像越接近越好。当然在实践中，我们为了保证高效训练，我们会将每一帧画面分割为很多块作为输入，并行分别进行预测。我们接下来为了简化，假设网络是一次性输入的整个画面。如果我们使用前几章介绍的基于监督学习的训练方法，我们得到的结果可能会是的十分模糊的甚至游戏中的角色消失、出现残影的，如图 8.3 所示。

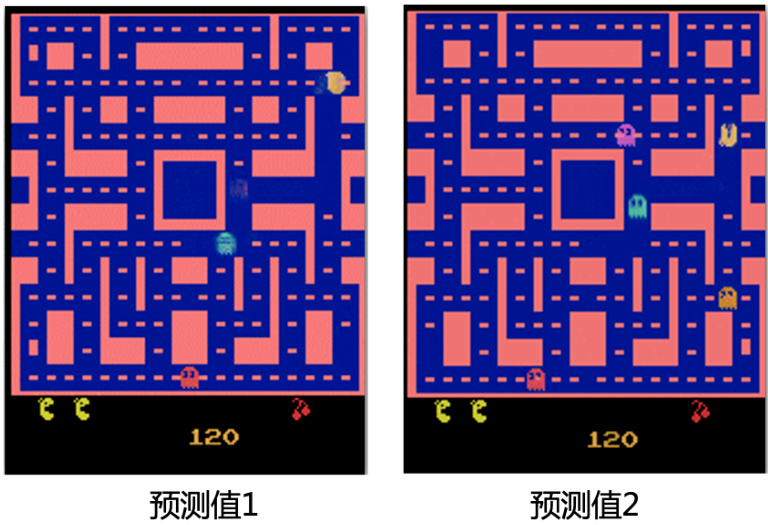
图 8.3 基于监督学习的小精灵游戏的预测值

造成该问题的原因是，我们监督学习中的训练数据对于同样的转角同时存储有角色向左转和向右转两种输出。当我们在训练的时候，对于一条向左转的训练数据，网络得到的指示就是要学会游戏角色向左转的输出。同理，对于一条向右转的训练数据，网络得到的指示就是学会角色向右转的输出。但是实际上这两种数据可能会被同时训练，所以网络就会学到的是“两面讨好”。当这个输出同时距离向左转和向右转最近，网络就会得到一个错误的结果—向左转是对的，向右转也是对的。

所以我们应该如何解决这个问题呢？答案是让网络有概率的输出一切可能的结果，或者说输出一个概率的分布，而不是原来的单一的输出，如图 8.4 所示。当我们给网络一个随机分布时，网络的输入会加上是一个 $z$ ，这时输出就变成了一个非固定的分布，其包含了向左转和向右转的可能。举例来说，假设我们选择的 $z$ 服从一个二项分布，即就只有 0 和 1 并且各占 $50\mathrm{\%}$ 。那么我们的网络就可以学到 $z$ 采样到 1 的时候就向左转，采样到 0 的时候就向右转，这样就可以解决了。

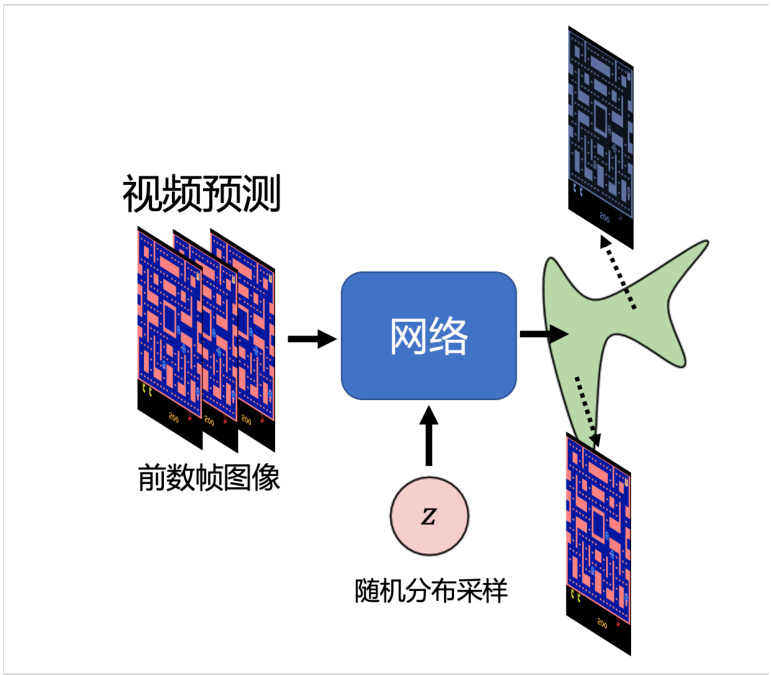
图 8.4 基于生成模型的小精灵游戏的预测结果

回到生成器的讨论中，我们什么需要这类的生成模型呢？答案是当我们的任务需要“创造性”的输出，或者我们想知道一个可以输出多种可能的模型，且这些输出都是对的模型的时候。这可以类比于，让很多人一起处理一个开放式的问题，或者是头脑风暴，大家的回答五花八门可以各自发挥，但是回答都是正确的。所以生成模型也可以被理解为让模型自己拥有了创造的能力。再举两个更具体的例子，对于画图，假设画一个红眼睛的角色，那每个人可能画出来或者心中想的动画人物都不一样。对于聊天机器人，它也需要有创造力。比如我们对机器人说，你知道有哪些童话故事吗？聊天机器人会回答安徒生童话、格林童话甚至其他的，没有一个标准的答案。所以对于我们的生成模型来说，其需要能够输出一个分布，或者说多个答案。当然在生成模型中，非常知名的就是生成式对抗网络（generative adversarial network），我们通常缩写为 GAN。这一节我们就讲介绍这个生成对抗网络。

我们通过让机器生成动画人物的面部来形象地介绍 GAN，首先介绍的是无限制生成（un-conditional generation），也就是我们不需要原始输入 $x$ 。其对应的就是需要原始输入 $x$ 的条件型生成（conditional generation）。如图 8.5 所示，对于无限制的 GAN，它的唯一输出就是 $z$ ，这里假设为正态分布采样出的向量。其通常是一个低维的向量，例如 50、100 的维度。

我们首先从正态分布中采样得到一个向量 $z$ ，并输入到生成器中，生成器会给我们一个对应的输出——一个动漫人物的脸。我们聚焦一下生成器输出一个动漫人物面部的过程。其实很简单，一张图片就是一个高维的向量，所以生成器实际上做的事情就是输出一个高维的向量，比如是一个 $64\times 64$ 的图片（如果是彩色图片那么输出就是 $64\times 64\times 3,$ ）。当输入的向量 $z$ 不同的时候，生成器的输出就会跟着改变，所以我们从正态分布中采样出不同的 $z$ ，得到的输出 $y$ 也就会不同，动漫人脸照片也不同。当然，我们也可以选择其他的分布，但是根据经验，分布之间的差异可能并没有非常大。大家可以找到一些文献，并且尝试去探讨不同的分布之间的差异。我们这里选择正态分布是因为其简单且常见，而且生成器自己会想方设法把这个简单的分布对应到一个更复杂的分布。所以我们后续的讨论都以正态分布为前提。

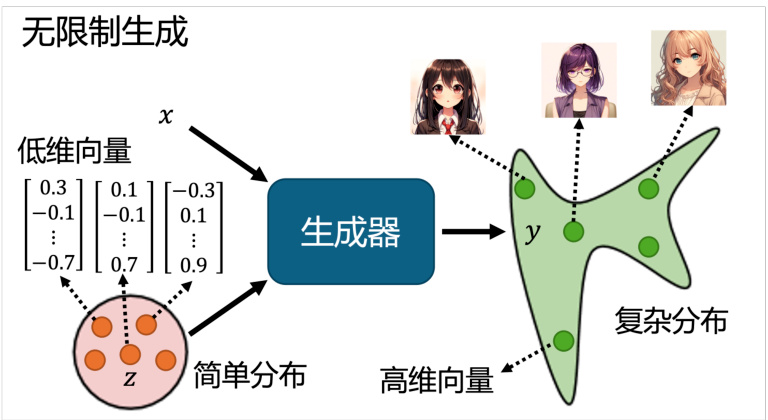
图 8.5 基于无限制生成的 GAN

8.1.2 辨别器

在 GAN 中，除了生成器以外，我们要多训练一个判别器（discriminator），其通常是一个神经网络。判别器会输入一张图片，输出一个标量，其数值越大就代表现在输入的图片越像是真实的动漫人物的图像，如图 8.6 所示。举例来说，对于图 8.6中的动漫人物头像，那输出就是 1。这里假设 1 是最大的值，画得很好的动漫图像输出就是 1，不知道在画什么就输出0.5，再差一些就输出 0.1 等等。判别器从本质来说与生成器一样也是神经网络，是由我们自己设计的，可以用卷积神经网络，也可以用 Transformer，只要能够产生出我们要的输入输出即可。当然对于这个例子，因为输入是一张图片，所以选择卷积神经网络，因为其在处理图像上有非常大的优势。

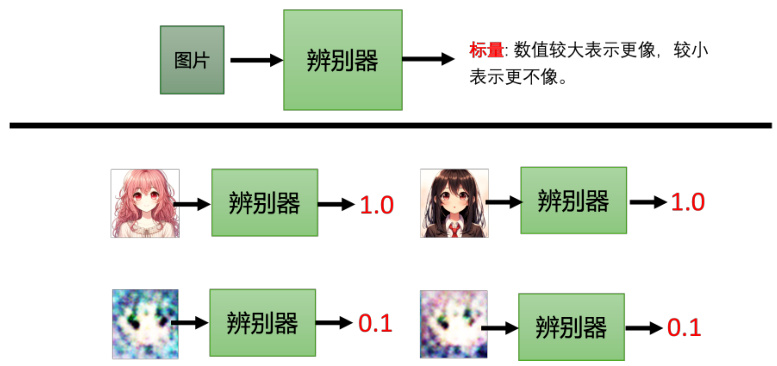
图 8.6 GAN 中的辨别器

我们回到动漫人物图片的例子，生成器学习画出动漫的人物的过程如图 8.7所示。首先，第一代生成器的参数几乎是完全随机的，所以它根本就不知道要怎么画动漫人物，所以其画出来的东西就是一些莫名其妙的噪音。那判别器学习的目标是成功分辨生成器输出的动漫图片。当然在图 8.7的例子里面可能非常容易，对判别器来说它只要看图片中是否有两个黑黑的眼睛即可。接下来生成器就要通过训练调整里面的参数来骗过判别器。假设判别器判断一张图片是不是真实图片的依据是看图片有没有眼睛，那新的生成器就需要输出有眼睛的图片。所以生成器产生眼睛出来，它是可以骗过第一代的判别器的。同时判别器也是会进化的，其会试图分辨新的生成器与真实图片之间的差异。例如，通过有没有嘴巴来识别真假。所以第三代的生成器就会想办法去骗过第二代的判别器，比如把嘴巴加上去。当然同时判别器也会逐渐的进步，会越来越严苛，来“逼迫”生成器产生出来的图片越来越像动漫的人物。所以生成器和判别器彼此之间是一直的互动、促进关系，和我们所说的“内卷”一样。最终，生成器会学会画出动漫人物的脸，而判别器也会学会分辨真假图片，这就是 GAN 的训练过程。

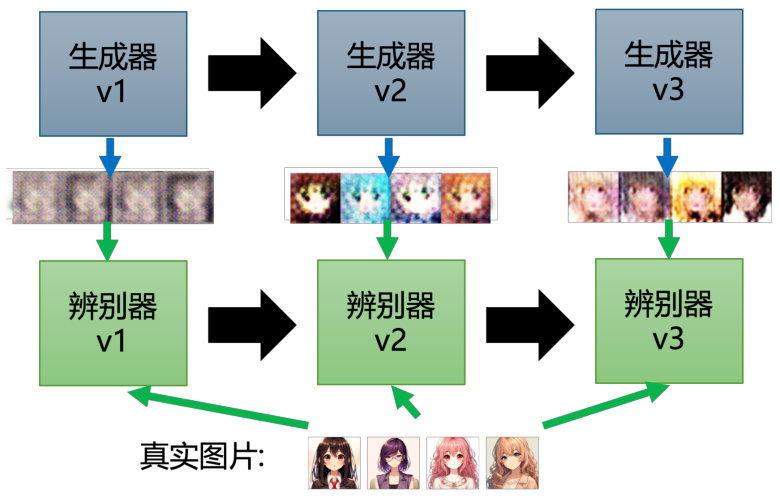
图 8.7 GAN 训练的过程

GAN 最早出现在 14 年的一篇文章中，其作者把生成器和判别器当作是敌人，并且生成器和判别器中间有一个对抗的关系，所以就用了一个“对抗”这个单词，当然这只是一个拟人化的说法而已。但是其实我们也可以把他们想为亦敌亦友的关系，毕竟它们一直在比这更新，比着提升自己，超越对方。

8.2 生成器与辨别器的训练过程

下面，我们从算法角度来解释生成器和判别器是如何运作的，如图 8.8所示。生成器和判别器是两个网络，在训练前我们要先分别进行参数初始化。训练的第一步是固定生成器，只训练判别器。因为生成器的初始参数是随机初始化的，所以它什么都没有学习到，输入一系列采样得到的向量给它，它的输出肯定都是些随机、混乱的图片，就像是坏掉的老式电视收不到信号时的花屏一样，与真实的动漫头像完全不同。同时，我们会有一个很多动漫人物头像的图像数据库，可以通过爬虫等方法得到。我们会从这个图库中采样一些动漫人物头像图片出来，来与生成器产生出来的结果对比从而训练判别器。判别器的训练目标是要分辨真正的动漫人物与生成器产生出来的动漫人物间的差异。具体来说，我们把真正的图片都标 1，生成器产生出来的图片都标 0。接下来对于判别器来说，这就是一个分类或回归的问题。如果是分类的问题，我们就把真正的人脸当作类别 1，生成器产生出来的图片当作类别 2，然后训练一个分类器。如果当作回归的问题，判别器看到真实图片就要输出 1，生成器的图片就要输出 0，并且进行 0-1 之间的打分。总之，判别器就学着去分辨这个真实图像和产生出来的图像间的差异。

我们训练完判别器以后，接下来第二步，固定判别器，训练生成器，如图 8.9所示。训练生成器的目的就是让生成器想办法去骗过判别器，因为在第一步中判别器已经学会分辨真图和假图间的差异。生成器如果可以骗过判别器，那生成器产生出来的图片可能就可以以假乱真。具体的操作如下：首先生成器输入一个向量，其可以来源于我们之前介绍的高斯分布中采

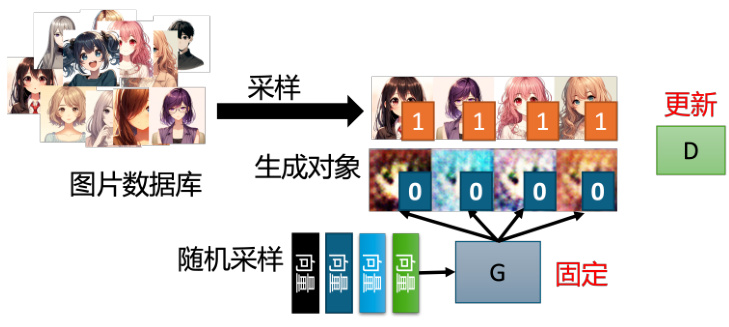
图 8.8 GAN 算法的第一步

辨别器学习给真实对象分配高分，给生成的对象分配低分。

样数据，并产生一个图片。接着我们将这个图片输入到判别器中，判别器会给这个图片一个打分。这里判别器是固定的，它只需要给更“真”的图片更高的分数即可，生成器训练的目标就是让图片更加真实，也就是提高分数。

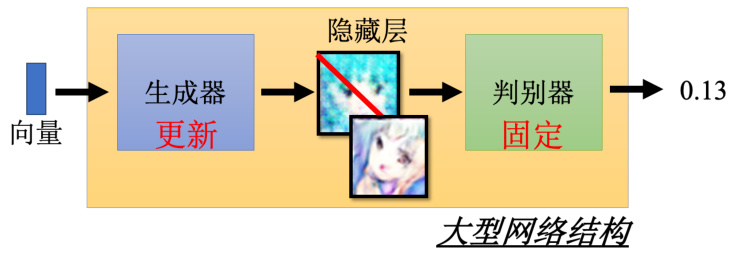
图 8.9 GAN 算法的第二步

对于真实场景中生成器和判别器都是有很多层的神经网络，我们通常将两者一起当作一个比较大的网络来看待，但是不会调整判别器部分的模型参数。因为假设要输出的分数越大越好，那我们完全可以直接调整最后的输出层，改变一下偏差值设为很大的值，那输出的得分就会很高，但是完全达不到我们想要的效果。所以我们只能训练生成的部分，训练方法与前几章介绍的网络训练方法基本一致，只是我们希望优化目标越大越好，这个与之前我们希望损失越小越好不同。当然我们也可以直接在优化目标前加“负号”，就当作损失看待也可以，这样就变为了让损失变小。另一种方法，我们可以使用梯度上升进行优化，而取代之前的梯度下降优化算法。

总结一下，GAN 算法的两个步骤。步骤一，固定生成器训练判别器；步骤二，固定判别器训练生成器。接下来就是重复以上的训练，训练完判别器固定判别器训练生成器。训练完生成器以后再用生成器去产生更多的新图片再给判别器做训练。训练完判别器后再训练生成器，如此反覆地去执行。当其中一个进行训练的时候，另外一个就固定住，期待它们都可以在自己的目标处达到最优，如图 8.10所示。

8.3 GAN 的应用案例

下面介绍一些 GAN 算法的应用。首先介绍 GAN 生成动画人物人脸的例子，如图 8.11所示。这些分别是训练 100 轮、1000 轮、2000 轮、5000 轮、10000 轮、20000 轮和 50000 轮的结果。我们可以看到训练 100 轮时，生成的图片还比较模糊；训练到 1000 轮的时候，机器就产生了眼睛；训练到 2000 轮的时候，嘴巴就生成出来了；训练到 5000 轮的时候，已经开始有一点人脸的轮廓了，并且机器学到了动画人物水汪汪大眼睛的特征；训练到 10000 轮以后，外部轮廓已经可以明显感觉到了，只是还有些模糊，有些水彩画感觉；更新 20000 轮后生成的图片完全可以以假乱真，并且 50000 轮后生成的图片已经十分逼真了。

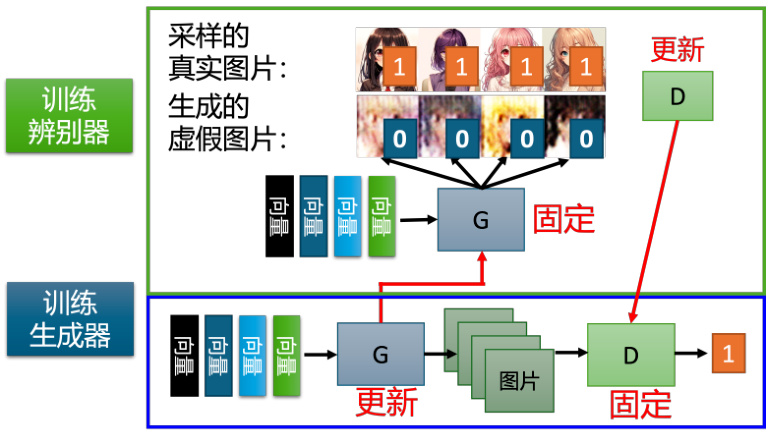
图 8.10 GAN 算法的完整训练过程

图 8.11 GAN 生成动画人物人脸的可视化效果

除了产生动画人物以外，当然也可以产生真实的人脸，如图 8.12产生高清人脸的技术，叫做渐进式 GAN（progressive GAN），上下两排都是由机器产生的人脸。

同样，我们可以用 GAN 产生我们从没有看过的人脸，如图 8.13所示。举例来说，先前我们介绍的 GAN 中的生成器，就是输入一个向量，输出一张图片。此外，我们还可以把输入的向量做内差，在输出部分我们就会看到两张图片之间连续的变化。比如我们输入一个向量通过 GAN 产生一个看起来非常严肃的男人，同时输入另一个向量通过 GAN 产生一个微笑着的女人。那我们输入这两个向量中间的数值向量，就可以看到这个男人逐渐地笑了起来。另一个例子，输入一个向量产生一个往左看的人，同时输入一个向量产生一个往右看的人，我们在之间做内差，机器并不会傻傻地将两张图片叠在一起，而是生成一张正面的脸。神奇的是，我们在训练的时候其实并没有真的输入正面的人脸，但机器可以自己学到把这两张左右脸做内差，应该会得到一个往正面看的人脸。

不过如果我们不加约束，GAN 会产生一些很奇怪的图片，如图 8.14所示。比如我们使用BigGAN 算法，会产生一个左右不对称的玻璃杯子，甚至产生一个网球狗，还是很有趣的。

图 8.12 渐进式 GAN 生成人脸的效果

图 8.13 GAN 产生连续人脸的过程

8.4 GAN 的理论介绍

这一小节我们将从理论层面介绍 GAN，即为什么生成器与判别器的交互可以产生人脸图片。首先，我们需要了解训练的目标是什么。在训练网络时，我们要确定一个损失函数，然后使梯度下降策略来调整网络参数，并使得设定的损失函数的数值最小或最大即可。在8.1中我们介绍了，生成器的输入是一系列的从分布中采样出的向量，生成器就会产生一个比较复杂的分布，如图 8.15 所示，我们称之为 $P_G$ 。另外我们还有一系列的数据，这些原始的数据本身会形成另外一个分布，我们称之为 $P_{data}$ 。训练的效果是希望 $P_G$ 和 $P_{data}$ 尽可能的相似。

我们再举一个一维的简单例子说明 $P_G$ 和 $P_{data}$ ，我们假设生成器的输入是一个一维的向量，如图 8.15的橙色曲线，生成器的输出也是一维的向量，如图 8.15的绿色曲线，真正的数据同样是一个一维的向量，它的分布用蓝色曲线来表示。假设每次我们输入 5 个点，那每一个点的位置就会随着训练次数而改变，就会产生一个新的分布。可能本来所有的点都集中在中间，但是通过生成器，通过一个网络里面很复杂的训练后，这些点就分成两边，变成图片中的分布的样子。而其中 $P_{data}$ 就是指真正数据的分布，在实际应用中真正数据分布可能是更极端的，比如左边的数据比较多，右边的数据比较少。我们训练的结果是希望两个分布 $P_G$ 和

图 8.14 GAN 产生不符合常理的可视化例子

$P_{data}$ 越接近越好，即图片中的公式所示，表达的是这两个分布之间的差异，我们可以将其视为两个分布间的某种距离，如果这个距离越大，就代表这两个分布越不像；差异越小，代表这两个分布越相近。所以差异就是衡量两个的分布相似度的一个指标。我们现在的目标就是训练一组生成器模型中的网络参数，可以让生成的 $P_G$ 和 $P_{data}$ 之间的差异越小越好，这个最优生成器称为 $G^{\ast }$ 。

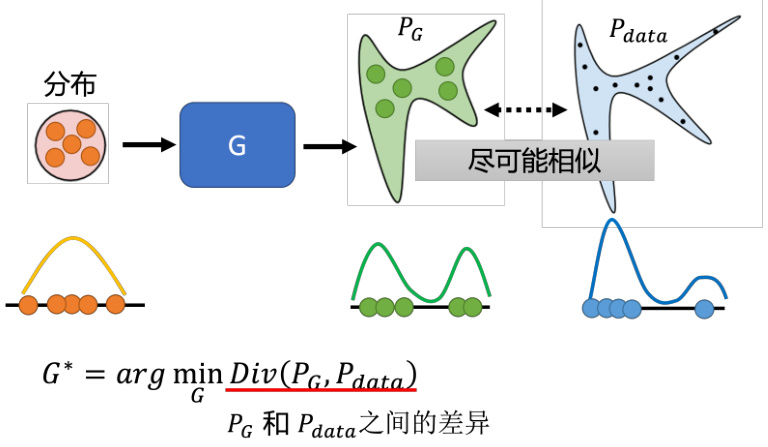
图 8.15 GAN 的训练目标

训练生成器的过程训练例如卷积神经网络等简单网络非常地像，相比于之前的找一组参数最小化损失函数，我们现在其实也定义了生成器的损失函数，即 $P_G$ 和 $P_{data}$ 之间的差异。对于一般的神经网络，其损失函数是可以计算的，但是对于生成器的差异，我们应该怎么处理呢？对于连续的差异例如 KL 散度和 JS 散度是很复杂的，在实际离散的数据中，我们或许无法计算其对应的积分。

对于 GAN，只要我们知道怎样从 $P_G$ 和 $P_{data}$ 中采样，就可以计算得到差异，而不需要知道实际的公式。例如，我们对于图库进行随机采样时，就会得到 $P_{data}$ 。对于生成器，我们需要从正态分布中采样出来的向量通过生成器生成一系列的图片，这些图片就是 $P_G$ 采样出来的结果。所以我们有办法从 $P_G$ 采样，也可以从 $P_{data}$ 进行采样。接下来，我们将介绍如何只做以上采样的前提下，即不知道 $P_G$ 和 $P_{data}$ 的形式以及公式的情况下，如何估算得到差异，这其中要依靠判别器的力量。

我们首先回顾下判别器的训练方式。首先，我们有一系列的真实数据，也就是从 $P_{data}$ 采样得到的数据。同时，还有一系列的生成数据，从 $P_G$ 中采样出来的数据。根据真实数据和生成数据，我们会去训练一个判别器，其训练目标是看到真实数据就给它比较高的分数，看到生成的数据就给它比较低的分数。我们可以把它当做是一个优化问题，具体来说，我们要训练一个判别器，其可以最大化一个目标函数，当然如果我们最小化它就可以称它为损失函数。这个目标函数如图 8.16所示，其中有一些 $y$ 是从 $P_{d}ata$ 中采样得到的，也就是真实的数据，而我们把这个真正的数据输入到判别器中，得到一个分数。另一方面，我们还有一些 $y$ 来源于生成器，即从 $P_G$ 中采样出来的，将这些生成图片输入至判别器中同样得到一个分数，再取$Log(1-D(Y))$ 。

我们希望目标函数 $V$ 越大越好，其中 $y$ 如果是从 $P_{data}$ 中采样得到的真实数据，它就要越大越好；如果是从 $P_G$ 采样得到的生成数据，它就要越小越好。这个过程在 GAN 提出之初，人们将其写为这样其实还有一个缘由，就是为了让判别器和二分类产生联系，因为这个目标函数本身就是一个交叉熵乘上一个负号。训练一个分类器时的操作就是要最小化交叉熵，所以当我们最大化目标函数的时候，其实等同于最小化交叉熵，也就是等同于是在训练一个分类器。这个它做的事情就是把图 8.16 中蓝色点，从 $P_{data}$ 采样出的真实数据当作类别 1，把从 $P_G$ 采样出的这些假的数据当作类别 2。有两个类别的数据，训练一个二分类的分类器，训练后就等同于是解了这个优化问题。而图中红框里面的数值，它本身就和 JS 散度有关。或许最原始的 GAN 的文章，它的出发点是从二分类开始的，一开始是把判别器写成二分类的分类器然后有了这样的目标函数，然后再经过一番推导后发现这个目标函数的最大值和 JS 散度是相关的。

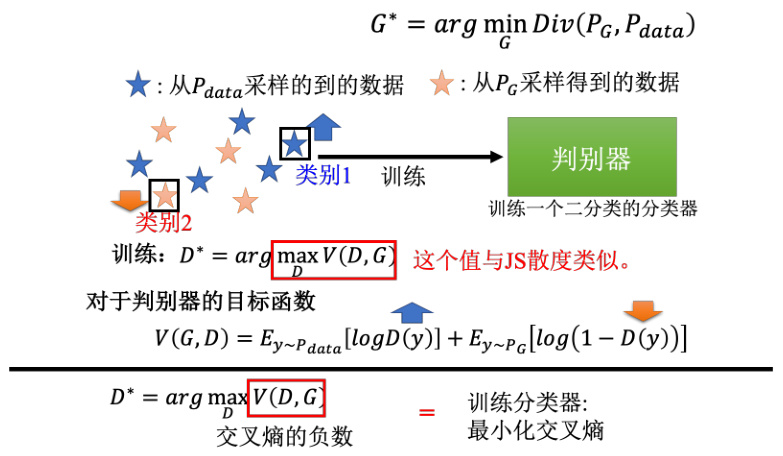
图 8.16 GAN 中判别器目标函数和优化过程

当然我们还是要直观理解下为什么目标函数的值会和散度有关。这里我们假设 $P_G$ 和$P_{data}$ 的差距很小，就如图 8.16 所示蓝色的星星和红色的星星混在一起。这里，判别器就是在训练一个 0、1 分类的分类器，但是因为这两组数据差距很小，所以在解决这个优化问题时，就很难让目标函数 $V$ 达到最大值。但是当两组数据差距很大时，也就是蓝色的星星和红色的星星并没有混在一起，那么就可以轻易地把它们分开。当判别器可以轻易把它们分开的时候，目标的函数就可以变得很大。所以当两组数据差距很大的时候，目标函数的最大值就可以很大。当然这里面有很多的假设，例如判别器的分类能力无穷大。

我们再来看下计算生成器 ${}^{+}$ 判别器的过程，我们的目标是要找一个生成器去最小化两个分布 $P_G$ 和 $P_{data}$ 的差异。这个差异就是使用训练好的判别器来最大化它的目标函数值来实现。最小和最大的 MinMax 过程就像是生成器和判别器进行互动，互相“欺骗”的过程。注意，这里的差异函数不一定使用 KL 或者 JS 等函数，可以尝试不同的函数来得到不同差异衡量指

标。

8.5 WGAN 算法

因为要进行 MinMax 操作，所以 GAN 是很不好训练的。我们接下来介绍一个 GAN训练的小技巧，就是著名的Wasserstein GAN（Wasserstein Generative AdversarialNetwork）。在讲这个之前，我们分析下 JS 散度有什么问题。首先，JS 散度的两个输入 $P_G$ 和 $P_{data}$ 之间的重叠部分往往非常少。这个其实也是可以预料到的，我们从不同的角度来看：图片其实是高维空间里低维的流形，因为在高维空间中随便采样一个点，它通常都没有办法构成一个人物的头像，所以人物头像的分布，在高维的空间中其实是非常狭窄的。换个角度解释，如果是以二维空间为例，图片的分布可能就是二维空间的一条线，也就是 $P_G$ 和 $P_{d}ata$ 都是二维空间中的两条直线。而二维空间中的两条直线，除非它们刚好重合，否则它们相交的范围是几乎可以忽略的。从另一个角度解释，我们从来都不知道 $P_G$ 和 $P_{d}ata$ 的具体分布，因为其源于采样，所以也许它们是有非常小的重叠分布范围。比如采样的点不够多，就算是这两个分布实际上很相似，也很难有任何的重叠的部分。

如果两个分布不重叠，JS散度总是Log2。

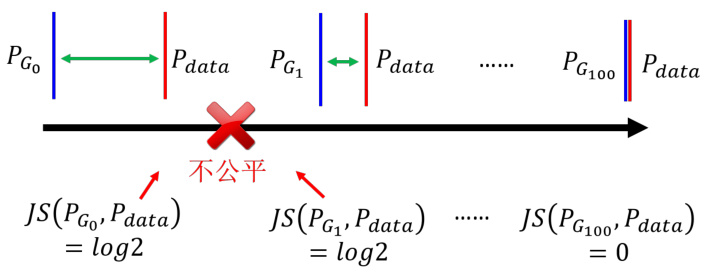
图 8.17 JS 散度的局限性

所以以上的问题就会对于 JS 分布造成以下问题：首先，对于两个没有重叠的分布，JS 散度的值都为 Log2，与具体的分布无关。就算两个分布都是直线，但是它们的距离不一样，得到的 JS 散度的值就都会是 Log2，如图 8.17 所示。所以 JS 散度的值并不能很好地反映两个分布的差异。另外，对于两个有重叠的分布，JS 散度的值也不一定能够很好地反映两个分布的差异。因为 JS 散度的值是有上限的，所以当两个分布的重叠部分很大时，JS 散度不好区分不同分布间的差异。所以既然从 JS 散度中，看不出来分布的差异。那么在训练的时候，我们就很难知道我们的生成器有没有在变好，我们也很难知道我们的判别器有没有在变好。所以我们需要一个更好的衡量两个分布差异的指标。

我们从更直观的实际操作角度来说明，当使用 JS 散度训练一个二分类的分类器，来去分辨真实和生成的图片时，会发现实际上正确率几乎都是 $100\mathrm{\%}$ 。原因在于采样的图片根本就没几张，对于判别器来说，采样 256 张真实图片和 256 张假的图片它直接用硬背的方法都可以把这两组图片分开。所以实际上如果用二分类的分类器训练判别器下去，识别正确率都会是$100\mathrm{\%}$ 。根本就没有办法看出生成器有没有越来越好。所以过去尤其是在还没有 WGAN 这样的技术时，训练 GAN 真的就很像盲盒。根本就不知道训练的时候，模型有没有越来越好，所以旧时的做法是每次更新几次生成器后，就需要把图片打印可视化出来看。然后就要一边吃饭，一边看图片生成的结果，然后跑一跑就发现内存报错了就需要重新再来，所以过去训练GAN 真的是很辛苦的。这也不像我们在训练一般的网络的时候，有个损失函数，然后那个损失值随着训练的过程慢慢变小，当我们看到损失值慢慢变小时，我们就放心网络有在训练。但是对于 GAN 而言，我们根本就没有这样的指标，所以我们需要一个更好的衡量两个分布差异的指标。否则只能够用人眼看，用人眼守在电脑前面看，发现结果不好，就重新用一组超参数调一下网络。

既然是 JS 散度的问题，肯定有人就想问说会不会换一个衡量两个分布相似程度的方式，就可以解决这个问题了呢？是的，于是就有了 Wasserstein，或使用 Wasserstein 距离的想法。Wasserstein 距离的想法如下，假设两个分布分别为 $P$ 和 $Q$ ，我们想要知道这两个分布的差异，我们可以想像有一个推土机，它可以把 $P$ 这边的土堆挪到 $Q$ 这边，那么推土机平均走的距离就是 Wasserstein 距离。在这个例子里面，我们假设 $P$ 集中在一个点， $Q$ 集中在一个点，对推土机而言，假设它要把 $P$ 这边的土挪到 $Q$ 这边，那它要平均走的距离就是 $D$ ，那么 $P$ 和 $Q$ 的 Wasserstein 距离就是 $D$ 。但是如果 $P$ 和 $Q$ 的分布不是集中在一个点，而是分布在一个区域，那么我们就要考虑所有的可能性，也就是所有的推土机的走法，然后看平均走的距离是多少，这个平均走的距离就是 Wasserstein 距离。Wasserstein 距离可以想象为有一个推土机在推土，所以 Wasserstein 距离也称为推土机距离（Earth Mover’s Distance，EMD）。所以 Wasserstein 距离的定义如图 8.18 所示。

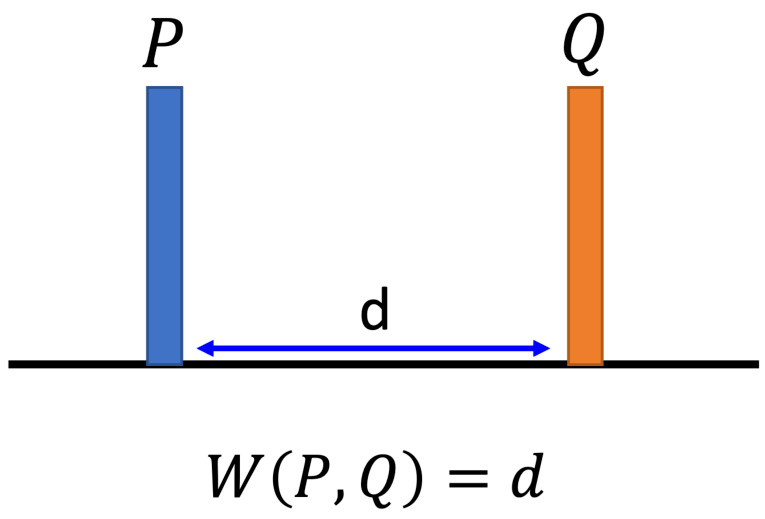
图 8.18 Wasserstein 距离的定义

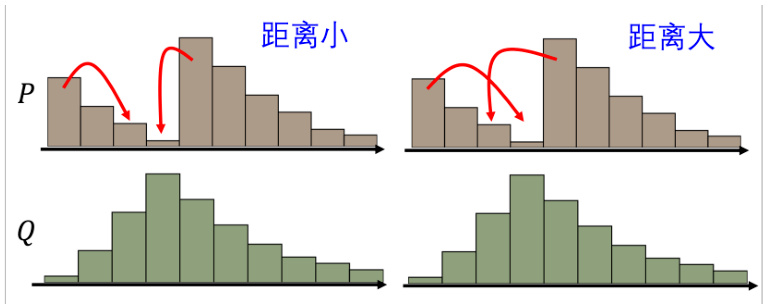
图 8.19 Wasserstein 距离的可视化理解

但是如果是更复杂的分布，要算 Wasserstein 距离就有点困难了，如图 8.19 所示。假设两个分布分别是 $P$ 和 $Q$ ，我们要把 $P$ 变成 $Q$ ，那有什么样的做法呢？我们可以把 $P$ 的土搬到 $Q$ 来，也可以反过来把 $Q$ 的土搬到 $P$ 。所以当我们考虑比较复杂分布的时候，两种分布计算距离就有很多不同的方法，即不同的“移动”方式，从中计算算出来的距离，即推土机平均走的距离就不一样。对于左边这个例子，推土机平均走的距离比较少；右边这个例子因为舍近求远，所以推土机平均走的距离比较大。那两个分布 $P$ 和 $Q$ 的 Wasserstein 距离会有很多不同的值吗？这样的话，我们就不知道到底要用哪一个值来当作是 Wasserstein 距离了。为了让 Wasserstein 距离只有一个值，我们将距离定义为穷举所有的“移动”方式，然后看哪一个推土的方法可以让平均的距离最小。那个最小的值才是 Wasserstein 距离。所以其实要计算Wasserstein 距离挺麻烦的，因为里面还要解一个优化问题。

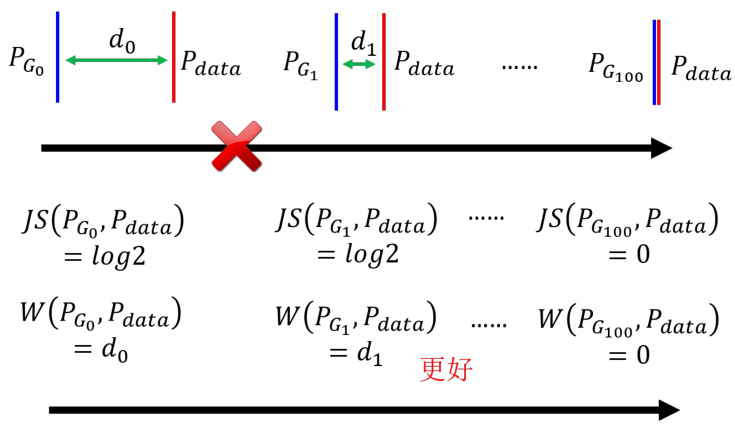
图 8.20 Wasserstein 距离与 JS 距离的对比

我们这里先避开这个问题，先来看看 Wasserstein 距离有什么好处，如图 8.20所示。假设两个分布 $P_G$ 和 $P_{data}$ 它们的距离是 $d_0$ ，那在这个例子中，Wasserstein 距离算出来就是 $d_0$ 。同样的，假设两个分布 $P_G$ 和 $P_{data}$ 它们的距离是 $d_1$ ，那在这个例子中，Wasserstein 距离算出来就是 $d_1$ 。假设 $d_1$ 小于 $d_0$ ，那 $d_1$ 的 Wasserstein 距离就会小于 $d_0$ 。所以 Wasserstein 距离可以很好地反映两个分布的差异。从左到右我们的生成器越来越进步，但是如果同时观察判别器，你会发现你观察不到任何规律。因为对于判别器而言，每一个例子算出来的 JS 散度，都是一样的 Log2，所以判别器根本就看不出来这边的分布有没有变好。但是如果换成 Wasserstein距离，由左向右的时候我们会知道，我们的生成器做得越来越好。所以我们的 Wasserstein 距离越小，对应的生成器就越好。这就是为什么我们要用 Wasserstein 距离的原因，我们换一个计算差异的方式，就可以解决 JS 距离有可能带来的问题。

可以再举一个演化的例子——人类眼睛的生成。人类的眼睛是非常复杂的，它是由其他原始的眼睛演化而来的。比如说有一些细胞具备有感光的能力，这可以看做是最原始的眼睛。那这些最原始的眼睛怎么变成最复杂的眼睛呢？它只是一些感光的细胞在皮肤上经过一系列的突变产生更多的感光细胞，中间有很多连续的步骤。举例来说，感光的细胞可能会出现在一个比较凹陷的地方，皮肤凹陷下去，这样感光细胞可以接受来自不同方向的光源。然后慢慢地把凹陷的地方保护住并在里面放一些液体，最后就变成了人的眼睛。所以这个过程是一个连续的过程，是一个从简单到复杂的过程。当使用 WGAN 时，使用 Wasserstein 距离来衡量分布间的偏差的时候，其实就制造了类似的效果。本来两个分布 $P_{G0}$ 和 $P_{data}$ 距离非常遥远，你要它一步从开始就直接跳到结尾，这是非常困难的。但是如果用 Wasserstein 距离，你可以让 $P_{G0}$ 和 $P_{data}$ 慢慢挪近到一起，可以让它们的距离变小一点，然后再变小一点，最后就可以让它们对齐在一起。所以这就是为什么我们要用 Wasserstein 距离的原因，因为它可以让我们的生成器一步一步地变好，而不是一下子就变好。

图 8.21 Wasserstein 距离的计算

所以 WGAN 实际上就是用 Wasserstein 距离来取代 JS 距离，这个 GAN 就叫做 WGAN。那接下来的问题是，Wasserstein 距离是要如何计算呢？我们可以看到，Wasserstein 距离的定义是一个最优化的问题，如图 8.21 所示。这里我们简化过程直接介绍结果，也就是解图中最大化问题的解，解出来以后所得到的值就是 Wasserstein 距离，即 $P_{G0}$ 和 $P_{data}$ 的 Wasserstein距离。我们观察一下图 8.21 的公式，即我们要找一个函数 $D$ ，这个函数 $D$ 是一个函数，我们可以想像成是一个神经网络，这个神经网络的输入是 $x$ ，输出是 $D(x)$ 。 $X$ 如果是从 $P_{data}$ 采样来的，我们要计算它的期望值 $E_{x\sim P_{data}}$ ，如果 $X$ 是从 $P_G$ 采样来的，那我们要计算它的期望值 $E_{x\sim P_G}$ ，然后再乘上一个负号，所以如果要最大化这个目标函数就会达成。如果 $X$ 如果是从 $P_{data}$ 采样得到的，那么判别器的输出要越大越好，如果 $X$ 如果是从 $P_G$ 采样得到的，从生成器采样出来的输出应该要越小越好。

此外还有另外一个限制。函数 $D$ 必须要是一个 1-Lipschitz 的函数。我们可以想像成，如果有一个函数的斜率是有上限的（足够平滑，变化不剧烈），那这个函数就是 1-Lipschitz 的函数。如果没有这个限制，只看大括号里面的值只单纯要左边的值越大越好，右边的值越小越好，那么在蓝色的点和绿色的点，也就是真正的图像和生成的图像没有重叠的时候，我们可以让左边的值无限大，右边的值无限小，这样的话，这个目标函数就可以无限大。这时整个训练过程就根本就没有办法收敛。所以我们要加上这个限制，让这个函数是一个 1-Lipschitz的函数，这样的话，左边的值无法无限大，右边的值无法无限小，所以这个目标函数就可以收敛。所以当判别器够平滑的时候，假设真实数据和生成数据的分布距离比较近，那就没有办法让真实数据的期望值非常大，同时生成的值非常小。因为如果让真实数据的期望值非常大，同时生成的值非常小，那它们中间的差距很大，判别器的更新变化就很剧烈，它就不平滑了，也就不是 1-Lipschitz 了。

那接下来的问题就是如何确保判别器一定符合 1-Lipschitz 函数的限制呢？其实最早刚提出 WGAN 的时候也没有什么好想法。最早的一篇 WGAN 的文章做了一个比较粗糙的处理，就是训练网络时，把判别器的参数限制在一个范围内，如果超过这个范围，就把梯度下降更新后的权重设为这个范围的边界值。但其实这个方法并不一定真的能够让判别器变成 1-Lipschitz 函数。虽然它可以让判别器变得平滑，但是它并没有真的去解这个优化问题，它并没有真的让判别器符合这个限制。

后来就有了一些其它的方法，例如说有一篇文章叫做 Improved WGAN，它就是使用了梯度惩罚（gradient penalty）的方法，这个方法可以让判别器变成 1-Lipschitz 函数。具体来说，如图 8.22 所示，假设蓝色区域是真实数据的分布，橘色是生成数据的分布，在真实数据这边采样一个数据，在生成数据这边取一个样本，然后在这两个点之间取一个中间的点，然后计算这个点的梯度，使之接近于 1。就是在判别器的目标函数里面，加上一个惩罚项，这个惩罚项就是判别器的梯度的范数减去 1 的平方，这个惩罚项的系数是一个超参数，这个超参数可以让你的判别器变得越平滑。在 Improved WGAN 之后，还有 Improved Improved WGAN，就是把这个限制再稍微改一改。另外还有方法是将判别器的参数限制在一个范围内，让它是1-Lipschitz 函数，这个叫做谱归一化。总之，这些方法都可以让判别器变成 1-Lipschitz 函数，但是这些方法都有一个问题，就是它们都是在判别器的目标函数里面加了一个惩罚项，这个惩罚项的系数是一个超参数，这个超参数会让你的判别器变得越平滑。

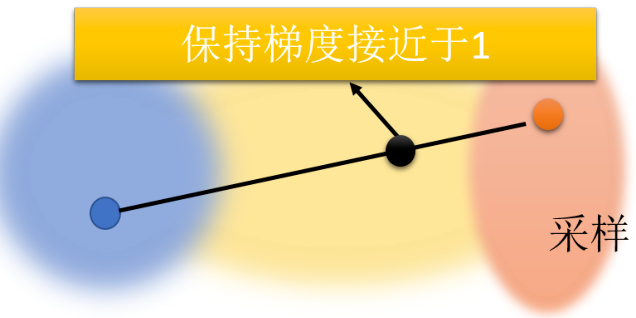
图 8.22 Improved WGAN 的梯度惩罚

8.6 训练 GAN 的难点与技巧

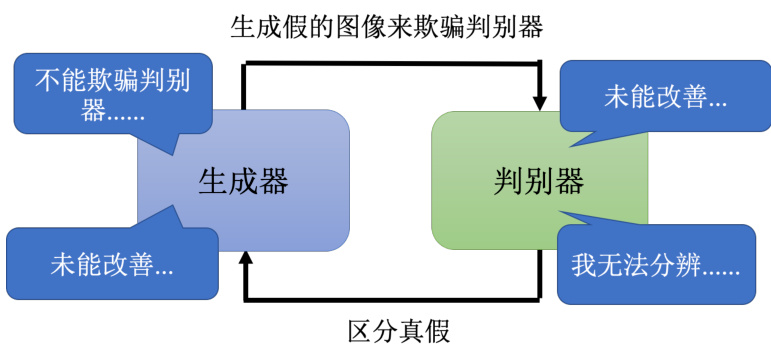
图 8.23 GAN 训练的难点

GAN 是以很难训练而闻名的，我们接下来介绍一些其中的原因和训练 GAN 的小技巧。首先，我们回顾一下判别器和生成器都在做些什么。判别器的目标是要分辨真的图片与产生出来的假图片间的差异，而生成器在做的事情是要去产生假的图片，骗过判别器。而事实上这两个网络，生成器和判别器它们是互相砥砺才能互相成长的，如图 8.23 所示。因为如果判别器太强了，那么生成器就会很难骗过它，生成器就会很难产生出真的图片。但是如果生成器太强了，那么判别器就会很难分辨真图片和假图片。只要其中一者发生什么问题停止训练，另外一个就会跟着停下训练就会跟着变差。假设在训练判别器的时候一下子没有训练好，那么判别器没有办法分辨真的跟产生出来的图片的差异，同时生成器就失去了可以进步的目标，生成器就没有办法再进步了。那么判别器也会跟着停下来，所以这两个网络是互相砥砺才能互相成长的。所以这也是为什么 GAN 很难训练的原因，因为这两个网络必须要同时训练，而且必须要同时训练到一个比较好的状态。

所以 GAN 本质上它的训练仍然不是一件容易的事情，当然它是一个非常重要的前瞻技术。有一些训练 GAN 的小技巧，例如 Soumith、DCGAN、BigGAN 等等。大家可以自己看看相关文献进行尝试。

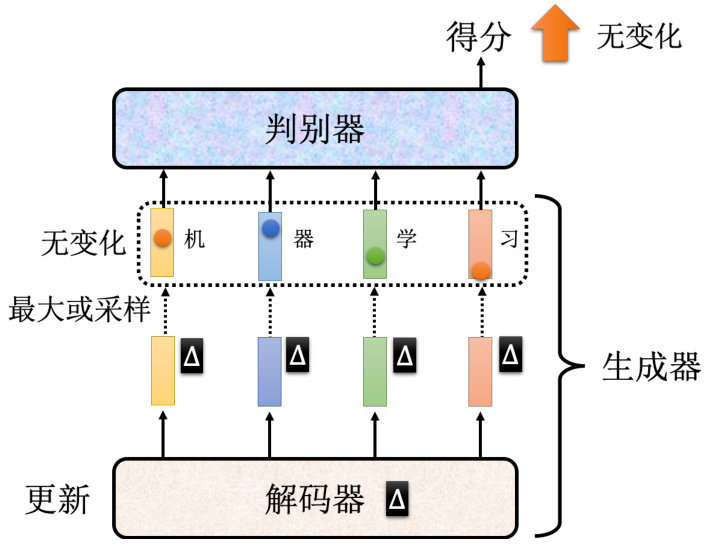
图 8.24 序列生成的 GAN

训练 GAN 最难的一个领域其实是要拿 GAN 来生成文字。如果要生成一段文字那需要一个序列到序列的模型，其中的一个解码器会产生一段文字，如图 8.24 所示。这个序列到序列的模型就是我们的生成器。著名的 Transformer 就是一个解码器，它现在在 GAN 里面，就扮演了生成器的角色，负责产生我们要它产生的东西，比如说一段文字。那这个序列到序列的GAN 和原来的用于图像中的 GAN 有什么不同呢？就最高层次来看，就算法来讲它们没有太大的不同。因为本质上就是训练一个判别器，判别器把这段文字读进去，去判断说这段文字是真正的文字还是机器产生出来的文字。而解码器就是想办法去骗过判别器，生成器就是想办法去骗过判别器，我们来调整生成器的参数，想办法让判别器觉得生成器产生出来的东西是真正的文字。所以从算法的角度来讲，它们没有太大的不同。对于序列到序列的模型其真正的难点在于，如果要用梯度下降去训练解码器，去让判别器输出得分越大越好，你会发现很难做到。我们来思考下，假设我们改变了解码器的参数，这个生成器，也就是解码器的参数，有一点小小的变化的时候，到底对判别器的输出有什么样的影响。如果解码器的参数有一点小小的变化，那它现在输出的分布也会有小小的变化，那因为这个变化很小，所以它对于输出的词元不会有很大的影响。

其中词元就是现在在处理产生这个序列的单位。假设我们今天，在产生一个中文的句子的时候，我们是每次产生一个汉字，那这每一个汉字就是我们的词元。在处理英文的时候，每次产生一个英文的字母，那字母就是你的词元。所以词元就是你产生一个序列的单位，那这个单位是你自己定义的。假设你一次是产生一个英文的词，英文的词和词之间是以空白分开的，那就是词就是你的词元。

我们回到刚才的讨论，假设输出的分布只有小小的变化，并且在取最大值的时候，或者说在找分数最大那个词元的时候，你会发现分数最大的那个词元是没有改变的。输出的分布只有小小的变化，所以分数最大的那个词元是同一个。那对于判别器来说，它输出的分数是没有改变的。判别器输出也不会改变，所以你根本就没有办法算微分，也根本就没有办法做梯度下降。当然就算是不能做梯度下降，我们还是可以用强化学习的方法来训练生成器。但是强化学习本身是以难训练而闻名，GAN 也是以难训练而闻名，这样的东西加在一起，就会非常非常地难训练。所以要用 GAN 产生一段文字，在过去一直被认为是一个非常大的难题。所以有很长一段时间，没有人可以成功地把生成器训练起来产生文字。

直到有一篇文章叫做 ScratchGAN，不需要预训练（pre-training），可以直接从随机的初始化参数开始，训练生成器，然后让生成器可以产生文字。它的方法是调节超参数，并且加上一些训练技巧，就可以从零开始训练生成器。里面的技巧比如说要用 SeqGAN-Step 的技术，并且将训练批大小设置的很大，要上千，然后要用强化学习的方法，要改一下强化学习的参数，同时加一些正则化等等技巧，就可以从真的把 GAN 训练起来，然后让它来产生序列。

此外，其实有关生成式的模型不是只有 GAN 而已，还有其他的比如 VAE，比如流模型等等，这些模型都有各自的优缺点。当然，就假设目前想要训练一个生成器，想让机器可以生成一些东西还是那有很多方法，可以用 GAN，可以 VAE，也可以用流模型。但是如果我们想要产生一些图片，那就最好用 GAN，因为 GAN 是目前为止比较好的生成式的模型，它可以产生最好的图片。但是如果想要产生一些文字，那就只有用 VAE 或者流模型，因为 GAN 在产生文字的时候，还是有一些问题。从训练角度，你可能会觉得 GAN 从式子上看起来有一个判别器和生成器，它们要互动。然后像流模型和 VAE 它们都比较像是直接训练一个一般的模型，有一个很明确的目标，不过实际上训练时它们也没有那么容易成功地被训练起来。因为它们的分类里面有很多项，它们的损失函数里面有很多项，然后把每一项都平衡才能够有好的结果，但要达成平衡也非常地困难。

那为什么我们需要用生成式来做输出新图片的事情呢？如果我们今天的目标就是，输入一个高斯分布的变量，然后使用采样出来的向量，直接输出一张照片，能不能直接用监督学习的方式来实现呢？具体做法比如我有一堆图片，每一个图片都去配一个向量，这个向量来源于从高斯分布中采样得到的向量，然后我就可以用监督学习的方式来训练一个网络，这个网络的输入是这个向量，输出是这个图片。确实能这么做，也真的有这样的生成式模型。但是难点在于，如果纯粹放随机的向量，那训练起来结果会很差。所以需要有一些特殊的方法例如生成式潜在优化等方法，供大家参考。

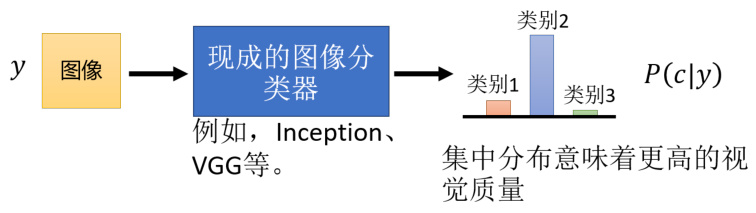
图 8.25 评估 GAN 生成图像的质量

8.7 GAN 的性能评估方法

接下来我们介绍 GAN 的评估方法，也就是我们产生出来的生成器它好或者是不好。要评估一个生成器的好坏，最直觉的做法也许是找人来看生成器产生出来的图片到底像不像真实的图片。所以其实很长一段时间，尤其是人们刚开始研究生成式技术的时候，很长一段时间没有好的评估方法。那时候要评估生成器的好坏，都是人眼看，直接在论文最后放几张图片，然后说这个生成器产生出来的图片是不是比较好。所以我们可以发现比较早年 GAN 的论文，它没有数字结果，整篇论文里面没有准确度等等的数字结果，它只有一些图片，然后说这个生成器产生出来的图片是不是比较好，接着就结束了。这样显然是不行的，并且有很多的问题，比如说不客观、不稳定等等诸多的问题。所以有没有比较客观而且自动的方法来度量一个生成器的好坏呢？

针对特定的一些任务，是有办法设计一些特定方法的。比如说我们要产生一些动画人物的头像，那我们可以设计一个专门用于动画人物面部的识别系统，然后看看我们的生成器产生出来的图片里面，有没有可以被识别的动画人物的人脸。如果有的话，那就代表说这个生成器产生出来的图片是比较好的。但是这个方法只能针对特定的任务，如果我们要产生的东西不是动画人物的头像，而是别的东西，那这个方法就不行了。那如果是更一般的案例，比如它不一定是产生动画人物的，它专门产生猫、专门产生狗、专门产生斑马等等，那我们怎么知道它做得好不好呢？

其实有一个方法，是训练一个图像的分类系统，然后把 GAN 产生出来的图片输入到这个图像的分类系统里面，看它产生什么样的结果，如图 8.25 所示。这个图像分类系统的输入是一张图片，输出是一个概率分布，这个概率分布代表说这张图片是猫的概率、狗的概率、斑马的概率等等。如果这个概率分布越集中，就代表现在产生的图片可能越好。如果生成出来的图片是一个四不像，图像识别系统就会非常地困惑，它产生出来的这个概率分布就会是非常平均地分布。

图 8.26 模式崩塌问题

这个是靠图像识别系统来判断产生出来的图片好坏，这是一个可能的做法，但是光用这个做法是不够的。光用这个做法会被一个叫做模式崩塌（mode collapse）的问题骗过去。模式崩塌是指在训练 GAN 的过程中遇到的一个状况，假设如图 8.26 蓝色的星星是真正的数据的分布，红色的星星是 GAN 的模型的分布。我们会发现生成式的模型它输出来的图片来来去去就是那几张，可能单一张拿出来你觉得好像还做得不错，但让它多产生几张就露出马脚，产生出来就只有那几张图片而已，这就是模式崩塌的问题。

发生模式崩塌的原因，从直觉上理解可以想成这个地方就是判别器的一个盲点，当生成器学会产生这种图片以后，它就永远都可以骗过判别器，判别器没办法看出来图片是假的。那对于如何避免模式坍塌，其实到今天其实还没有一个非常好的解答，不过有方法是模型在生成器训练的时候，一直将训练的节点存下来，在模式坍塌之前把训练停下来，就只训练到模式崩塌前，然后就把之前的模型拿出来用。不过模型崩塌这种问题，我们至少是知道有这个问题，是可以看得出的，生成器总是产生这张脸的时候，你不会说你的生成器是个好的生成器。但是有一些问题是你不知道的并且更难侦测到的，即你不知道生成器产生出来的图片是不是真的有多样性。

这个问题叫做模式丢失，指 GAN 能很好地生成训练集中的数据，但难以生成非训练集的数据，“缺乏想象力”。你的产生出来的数据，只有真实数据的一部分，单纯看产生出来的数据，你可能会觉得还不错，而且分布的这个多样性也够，但你不知道真实数据的多样性的分布其实是更大的。事实上今天这些非常好的 GAN，BGAN、ProgressGAN 等等可以产生非常真实人脸这些 GAN，多多少少还是有模式丢失的问题。如果你看多了 GAN 产生出来的人脸，你会发现虽然非常真实但好像来来去去就是那么几张脸而已，并且有一个非常独特的特征是你看多了以后就觉得，这个脸好像是被生成出来的。今天也许模式丢失都还没有获得本质上的解决。

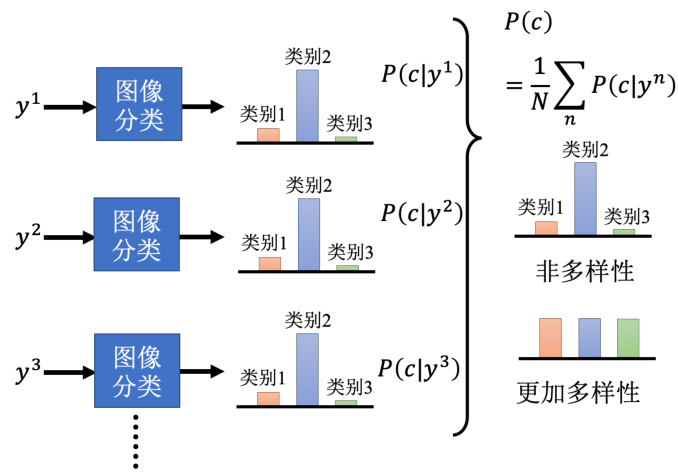
图 8.27 GAN 生成结果多样性问题

虽然存在以上模式坍塌、模式丢失等等的问题，但是我们需要去度量生成器产生出来的图片到底多样性够不够。有一个做法是借助我们之前介绍过的图像分类，把一系列图片都丢到图像分类器里，看它被判断成哪一个类别，如图 8.27 所示。每张图片都会给我们一个分布，我们将所有的分布平均起来，接下来看看平均的分布长什么样子。如果平均的分布非常集中，就代表现在多样性不够，如果平均的分布非常平坦，就代表现在多样性够了。具体来讲，如果什么图片输入到图像分类系统中的输出都是第二种类别，那代表说每一张图片也许都很像，也就代表输出的多样性是不够的，那如果另外一个案例不同张图片丢进去，它的输出分布都不一样，那就代表说多样性是够的。并且平均完以后发现结果是非常平坦的，那这个时候代表多样性是足够的。

当我们用这个图像分类器来做评估的时候，对于结果的多样性和质量好像是有点互斥的。因为我们刚才在讲质量的时候说，分布越集中代表质量越高，多样性的分布越平均。但是如果分布越平均，那质量就会越低，因为分布越平均，代表图片都不太像，所以质量就会越低。这里要强调一下质量和多样性的评估范围不一样，质量是只看一张图片，一张图片丢到分类器的时候，分布有没有非常地集中。而多样性看的是一堆图片分布的平均，一堆图片中图像分类器输出的越平均，那就代表现在的多样性越大。

过去有一个非常常被使用的分数，叫做 Inception 分数。其顾名思义就是用 Inception 网络来做评估，用 Inception 网络度量质量和多样性。如果质量高并且多样性又大，那 Inception分数就会比较大。目前研究人员通常会采取另外一个评估方式，叫 Fréchet Inception distance(FID)。具体来讲，先把生成器产生出来的人脸图片，丢到 InceptionNet 里面，让 Inception网络输出它的类别。这里我们需要的不是最终的类别，而是进入 Softmax 之前的隐藏层的输出向量，这个向量的维度是上千维的，代表这个图片，如图 8.28 所示。图中所有红色点代表把真正的图片丢到 Inception 网络以后，拿出来的向量。这个向量其实非常高维度，甚至是上千维的，我们就把它降维后画在二维的平面上。蓝色点是 GAN 的生成器产生出来的图片，它丢到 Inception 网络以后进入 Softmax 之前的向量。接下来，我们假设真实的图片和生成的图片都服从高斯分布，然后去计算这两个分布之间的 Fréchet 的距离。两个分布间的距离越小越好，距离越小越代表这两组图片越接近，也就是产生出来的品质越高。这里还有几个细节问题，首先，假设为高斯分布没问题吗？另外一个问题是如果要准确的得到网络的分布，那需要产生大量的采样样本才能做到，这需要一点运算量，也是做 FID 不可避免的问题。

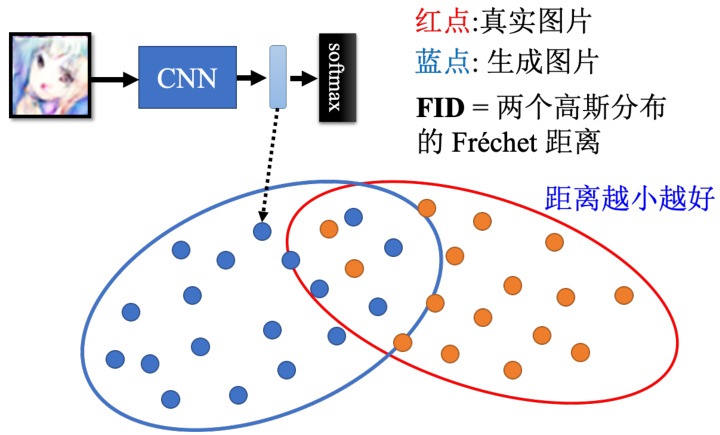
图 8.28 FID 的计算过程

FID 算是目前比较常用的一种度量方式，那有一篇文章叫做“Are GANs Created Equal?A Large-Scale Study”，这个 Google 完成的论文里面尝试了不同的 GAN。每一个 GAN 的训练的分类，训练的损失都有点不太一样，并且每一种 GAN，它都用不同的随机种子，去跑过很多次以后，取结果的平均值等等。从文章的结果来看所有的 GAN 都差不多，那所以与 GAN有关的研究都是白忙一场吗？事实上也未必是如此，这篇文章做实验的时候不同的 GAN 用的网络架构都是同一个，只是疯狂调参而已，调随机种子和学习率而已。网络架构还是同一个，所以是不是有某些网络架构，某些种类的 GAN 会不会在不同的网络架构上表现得比较稳定。这些都有待研究。

此外，还有一个状况。假设 GAN 产生出来的图片，跟真实的图片长得一模一样，那此时FID 会是零，因为两个分布是一模一样的。如果你不知道真实数据长什么样子，光看这个生成器的输出可能会觉得太棒了，那 FID 算出来一定是非常小的，但是如果它产生出来的图片都跟数据库里面的训练数据的一模一样的话，那干脆直接从训练数据集里面采样一些图像出来不是更好，也就不需要训练生成器了。我们训练生成器其实是希望它产生新的图片，也就是训练集里面没有的人脸。

对于这种问题，就不是普通的度量标准可以侦测的。那怎么解决呢？其实有一些方法，例如可以用一个分类器，这个分类器是用来判断这张图片是不是真实的，是不是来自于你的训练集的。这个分类器的输入是一张图片，输出是一个概率，这个概率代表说这张图片是不是来自于你的训练集。如果这个概率是 1，那就代表说这张图片是来自于你的训练集，如果这个概率是 0，那就代表说这张图片不是来自于你的训练集。但是另外一个问题，假设生成器学到的是把所有训练数据里面的图片都左右反转呢，那它也是什么事都没有做。但是你的分类器会觉得说，这张图片是来自于你的训练集，因为它是来自于你的训练集的图片，只不过是左右反转而已。进行分类时或者进行相似度的比较时，又比不出来。所以 GAN 的评估是非常地困难的，还甚至如何评估一个生成器做得好不好都是一个可以研究的题目。

8.8 条件型生成

下面，我们要介绍条件型生成（conditional generation）。我们之前讲的 GAN 中的生成器，它没有输入任何的条件，它只是输入一个随机的分布，然后产生出来一张图片。我们现在想要更进一步的是希望可以操控生成器的输出，我们给它一个条件 $x$ ，让他根据条件 $x$ 跟输入 $z$ 来产生输出 $y$ 。那这样的条件型生成器有什么样的应用呢？比如可以做文字对图片的生成，那如果要做文字对图片的生成，它其实是一个监督学习的问题，我们需要一些有标签的数据，需要去搜集一些人脸图片，然后这些人脸都要有文字的描述。比如这个样本是红眼睛、黑头发，另一个是黄头发、有黑眼圈等等标签的样本，才能够训练这种条件型生成器。所以在文字变图像这样的任务里面，我们的条件 $x$ 就是一段文字。我们希望输入一段文字，然后生成器就可以产生出来一张图片，这张图片就是这段文字所描述的图片。那一段文字怎么输入给生成器呢，其实依赖于你自己。以前会用 RNN 把它读过去，然后得到一个向量，再丢到生成器中。今天也许你可以把它丢到一个 Transformer 的编码器中，然后得到一个向量，再丢到生成器中，只要能够让生成器读一段文字就行。我们期待的模型是输入“红眼睛”，然后机器就可以画一个红眼睛的角色，而且每次画出来的角色都不一样。那这个画出来什么样的角色，取决于你采样到到什么样的 $z$ 。采样到不一样的 $z$ ，就会画出不一样的角色，但是这个角色都是红眼睛的。那这个就是条件型生成的应用，文字变图像。

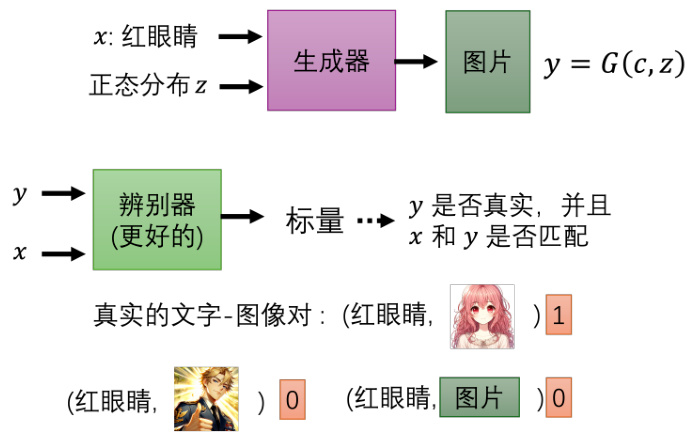
图 8.29 条件型 GAN

具体怎么做条件型的 GAN 呢？我们现在的生成器有两个输入，一个是正态分布中采样出来的 $z$ ，另一个是条件 $x$ 也就是一段文字，然后它会产生出来一个 $y$ ，也就是一张图片。同时，我们需要一个判别器。如果按照我们过去介绍的知识，判别器就是使用一张图片 $y$ 当作输入，输出一个数值，这个数值代表输入的图片多像真实的图片。训练这个判别器的方法就是，如果看到真实的图片就输出 1，如果看到生成的图片就输出 0。这样就可以训练判别器，然后判别器跟生成器反复训练。

但是这样的方法没办法真的解条件型的 GAN 的问题，因为如果我们只有训练这个判别器，只会将 $y$ 当做输入的话，那生成器会学到的东西就是，只要产生出来的图片 $y$ 好，但是跟输入完全没有任何关系，因为对生成器来说它只要产生清晰的图片就可以骗过判别器了。它何必要去管输入的文字叙述是什么呢，所以直接就无视这个条件 $x$ ，直接产生一个图片骗过判别器就结束了。但这显然不是我们要的，所以在条件型的 GAN 里面，就要做有点不一样的设计，也就是判别器不是只吃图片 $y$ ，同时还要吃条件 $x$ 。同时判别器输出的数值不只是看 $y$ 好不好，还要看 $y$ 跟 $x$ 配不配。如果 $y$ 跟 $x$ 配不上，那就要给一个很低的分数，如果 $y$ 跟$x$ 配上，那就要给一个很高的分数。我们需要文字和图像成对的数据来训练判别器，所以条件型的 GAN，一般的训练是需要这个成对的标注数据的。所以当看到这些真正的成对数据，就给它 1 分，看到红色眼睛但是文字叙述是黑色头发，就给它 0 分，看到黑色头发但是文字叙述是红色眼睛，也给它 0 分，这样就可以训练判别器了，如图 8.29 所示。

那其实在实际操作中，只是拿这样的负样本对和正样本对来训练判别器，得到的结果往往不够好。往往还需要加上一种不好的状况：已经产生好的图片但是文字叙述配不上的状况。所以通常会把我们的训练数据拿出来，然后故意把文字跟图片乱配，或者故意配一些错的，然后告诉判别器看到这种状况，也是要输出不匹配。用这样子的数据，才有办法把判别器训练好。然后生成器跟判别器反复的训练，最后才会得到好的结果，这个就是条件型的 GAN。

在目前的例子里面都是看一段文字产生图片，当然条件型的 GAN 的应用不只看一段文字产生图片，比如也可以看一张图片产生其他图片。比如，给 GAN 房屋的设计图，然后让生成器直接把房屋产生出来，或者给它黑白的图片然后让它把颜色着上，或者给它素描的图，让它把它变成实景实物，再或者给它白天的图片，让它变成晚上的图片，给它起雾的图片，让它变成没有雾的图片等等。那像这样子的应用，叫做图像翻译，也就是输入一张图片，然后产生出来另外一张图片，也叫做 Pix2pix。那跟刚才讲的从文字产生图像也没有什么不同，现在只是从图像产生图像，把文字的部分用图像取代掉而已。所以其中同样要产生生成器，产生一张图片，然后要产生判别器，判别器要输入两张图片，然后输出一个数值。其中可以用监督学习的方法，训练一个图片生成图片的生成器，但是可能生成的结果图片非常地模糊，原因在于同样的输入可能对应到不一样的输出。生成器学到的就是把不同的可能平均起来，结果变成一个模糊的结果。所以这个时候我们的判别器它是输入是一张照片和输入条件，同时看图片和条件看有没有匹配来决定它的输出。另外，如果单纯用 GAN 的话它有一个小问题，它产生出来的图片比较真实，但是与此同时它的创造力、想像力过度丰富，会产生一些输入没有的东西。所以如果要做到最好往往就是 GAN 跟监督学习同时使用，就是说你的生成器不只要骗过判别器，同时你的生成器还要产生出来的图片跟标准答案越像越好。

条件型 GAN 还有很多应用，比如给 GAN 听一段声音，然后产生一个对应的图片。比如说给它听一段狗叫声，GAN 可以画出一只狗。这个应用的原理跟刚才讲的文字变图像是一样的，只是输入的条件变成声音而已。对于标签的成对数据就是声音和图像成对的数据，这个并没有很难搜集，因为可以爬到大量的影片，影片里面有图像有画面也有声音，并且每一帧是一一对应的，所以可以用这样的数据来训练。另外条件型 GAN 还可以产生会动的图片，比如给GAN 一张蒙娜丽莎的画像，然后就可以让蒙娜丽莎开始讲话等等。

8.9 Cycle GAN

这一小节，我们要介绍一个 GAN 的另一个有趣的应用，就是把 GAN 用在无监督学习上。到目前为止呢，我们介绍的几乎都是监督学习，即我们要训练一个网络，其输入是 $x$ ，输出为 $y$ ，并且我们需要成对的数据才有办法训练网络。但是我们可能会遇到一个状况是，我们有一系列的输入和输出，但是 $x$ 和 $y$ 之间并没有成对的关系，也就是说我们没有成对的数据。举一个例子，比如图像风格转换的情况我们就没有成对的数据。我们有一系列真实的照片，然后有一些动漫的头像，我们希望可以把真实的照片转换成动漫的头像。具体来讲，假设我们要训练一个深度学习的网络，它要做的事情是把 $x$ 域的真人照片，转换为 $y$ 域的动漫人物的头像。在这个例子里面我们或许就没有任何的成对的数据，因为我们有一堆真人的照片，但是我们没有这些真人的动漫头像。除非我们将动漫的头像先自己画出来，我们才有办法训练网络，不过这个做法显然实在是太昂贵了。所以对于图像风格转换，我们可能一点成对的数据都没有。那么在这种状况下，还有没有办法训练一个网络输入一个 $x$ 产生一个 $y$ 呢？这个时候就可以用到 GAN，在这种完全没有成对数据的情况下进行学习。

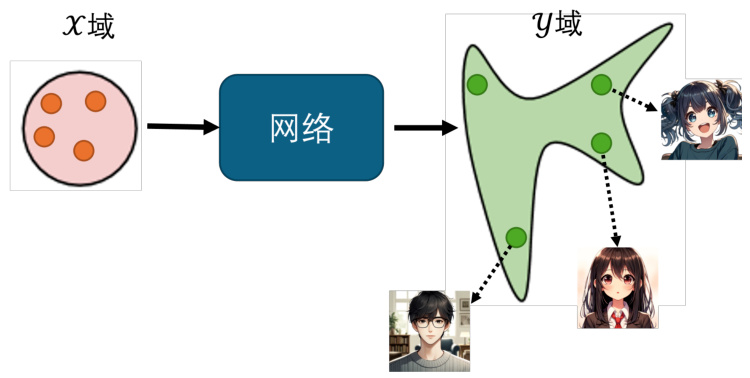
图 8.30 从无成对数据中学习的 GAN

如图 8.30 ，这个是我们之前在介绍无条件生成的时候所使用的生成器架构，输入是一个高斯的分布，输出可能是一个复杂的分布。现在稍微转换一下我们的想法，输入不是高斯分布，而是 $x$ 域的图片的分布， $y$ 域是图片的分布。我们完全可以套用原来的 GAN 的想法，即在原来的 GAN 中从高斯分布中采样一个向量输入到生成器里面，之前输入是 $x$ 域的分布，我们只要改成可以从 $x$ 域中采样就可以了。其实都不一定要从高斯分布采样，只要是一个分布，我们都可以从这个分布中采样一个向量丢到生成器里面，我们选择高斯分布只是因为它的公式我们是知道的。这个采样过程可以理解为就从真实的人脸里面随便挑一张出来，然后把这个照片丢到生成器里面，让它产生另外一张图片（分布)。这个时候我们的判别器就要改一下，判别器不再是只输入 $y$ 域的图片，而是同时输入 $x$ 域的图片和 $y$ 域的图片，然后输出一个数值，这个数值代表这两张图片是不是一对的。

这整个过程与之前的 GAN 没有什么区别，但是仔细想想看只是套用原来的 GAN 训练，好像是不够的。因为我们要做的事情是要让这个生成器输出一张 $y$ 域的图，但是它输出的 $y$ 域的图一定要跟输入有关系吗？此处我们没有做任何的限制，所以生成器也许就把这张图片当作一个符合高斯分布的噪音，然后不管你输入什么它都无视它，只要判别器觉得它做得很好就可以了。所以如果我们完全只套用一般 GAN 的做法，只训练一个生成器，这个生成器输入的分布从高斯分布变成 $x$ 域的图片，然后训练一个判别器，这样显然是不够的。因为训练出来的生成器，它可以产生的人物头像跟输入的真实的照片没有什么特别的关系，这个也不是我们要的。

那怎么解决这个问题呢？怎么强化输入与输出的关系呢？我们在介绍条件型 GAN 的时候，提到说假设判别器只看 $y$ ，那它可能会无视生成器的输入，所以产生出来的结果不是我们要的。所以我们要让判别器看 $x$ 和 $y$ ，这样才可以让生成器学到 $x$ 和 $y$ 之间的关系。但是目前如果我们要从没有样本对的数据中学习，我们也没有办法直接套用条件型 GAN 的想法，因为在条件型 GAN 里面我们是有成对的数据的，可以用这些成对的数据来训练的判别器。但目前我们没有成对的数据来告诉判别器，怎么样的 $x$ 和 $y$ 的组合才是对的。为了解决这个问题，我们可以使用循环生成对抗网络（Cycle GAN）。

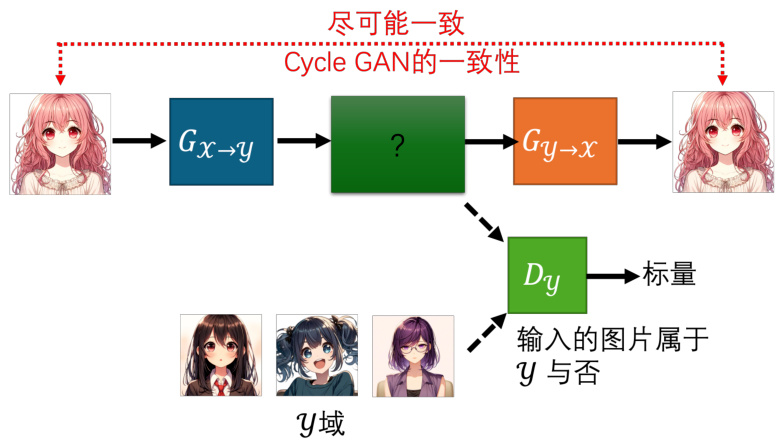
图 8.31 Cycle GAN 的基本架构

具体来说，在 Cycle GAN 中，我们会训练两个生成器。第一个生成器是把 $x$ 域的图变成$y$ 域的图，第二个生成器它的工作是看到一张 $y$ 域的图，把它还原回 $x$ 域的图。在训练的时候，我们会增加一个额外的目标，就是我们希望输入一张图片，其从 $x$ 域转成 $y$ 域以后，要从 $y$ 域转回原来一模一样的 $x$ 域的图片。就这样经过两次转换以后，输入跟输出要越接近越好，或者说两张图片对应的两个向量之间的距离越接近越好。因为这边有一个循环，从 $x$ 到$y$ 再从 $y$ 回到 $x$ ，所以它是一个循环，所以被称为 Cycle GAN。而因为输入经过两次转换以后变成输出，并且需要保证输入跟输出越接近越好，所以这个过程也被称为 Cycle GAN 的一致性。所以在 Cycle GAN 中我们有三个网络，第一个生成器的工作是把 $x$ 转成 $y$ ，第二个生成器的工作是要把 $y$ 还原回原来的 $x$ ，另一个判别器的工作仍然是要看第一个生成器的输出像不像是 $y$ 域的图，如图 8.31 所示。

那加入了第二个生成器以后，对于前面这个第一个的生成器来说，它就不能够随便产生与输入没有关系的人脸了。因为如果它产生出来的人脸跟输入的人脸没有关系，那第二个生成器就无法把它还原回原来的 $x$ 域的图片。所以对第一个生成器来说，为了要让第二个生成器能够成功还原原来的图片，它产生出来的图片就不能跟输入差太多，然后第二个生成器才能够还原回原来的输入。

另外有一个问题，我们需要只保证第一个生成器的输出和输入有一定的关系，但是我们怎么知道这个关系是所需要的呢？机器自己有没有可能学到很奇怪的转换并且满足 cycle 的一致性呢？比如一个很极端的例子，假设第一个生成器学到的是把图片左右翻转，那只要第二个生成器学到把图片左右翻转就可以还原了啊。这样的话，第一个生成器学到的东西跟输入的图片完全没有关系，但是第二个生成器还是可以还原回原来的图片。所以如果我们做 CycleGAN，用 cycle 的一致性的话似乎没有办法保证我们输入跟输出的人脸看起来很像，因为也许机器会学到很奇怪的转换，反正只要第二个生成器可以转得回来就好了。面对这个问题目前确实没有什么特别好的解法，但实际上使用 Cycle GAN 的时候，这种状况没有那么容易出现。输入和输出往往真的就会看起来非常像，甚至实际应用时就算没有第二个生成器，不用cycle GAN，使用一般的 GAN 替代这种图片风格转换的任务，往往效果也很好。因为网络其实非常“懒惰”，输入一个图片它往往就想输出默认的与输入很像的东西，它不太想把输入的图片做太复杂的转换。所以在实际应用中，Cycle GAN 的效果往往非常好，而且输入和输出往往真的就会看起来非常像，或许只是改变了风格而已。

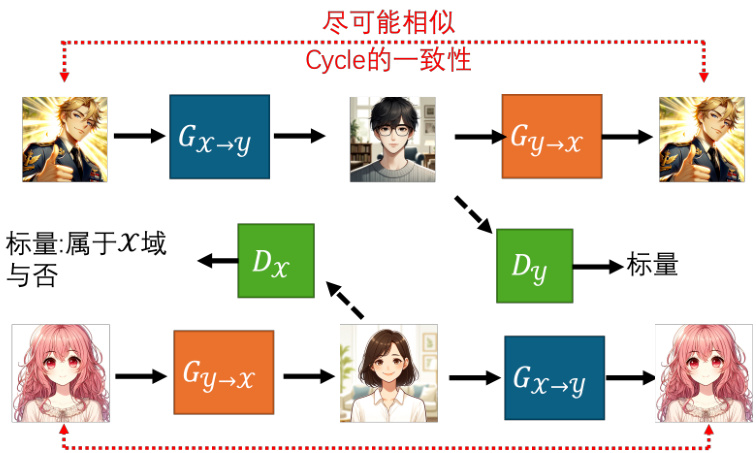
图 8.32 Cycle GAN 的双向架构

另一个角度，Cycle GAN 可以是双向的，如图 8.32 所示。我们刚才有一个生成器，输入$y$ 域的图片，输出 $x$ 域的图片，是先把 $x$ 域的图片转成 $y$ ，在把 $y$ 转回 $x$ 。在训练 cycle GAN的时候，其实可以同时做另外一个方向的训练，也就是把橙色的生成器给它 $y$ 域的图片，让它产生 $x$ 域的图片。然后在让蓝色的生成器把 $x$ 域的图片还原回原来 $y$ 域的图片。同时我们依然希望输入跟输出越接近越好，所以一样要训练一个判别器，这个判别器是 $x$ 域的判别器，它是要看橙色生成器输出的图片像不像是真实人脸的图片。这个橙色的生成器它要去骗过这个 $D_x$ 判别器。这个合起来就是 Cycle GAN。

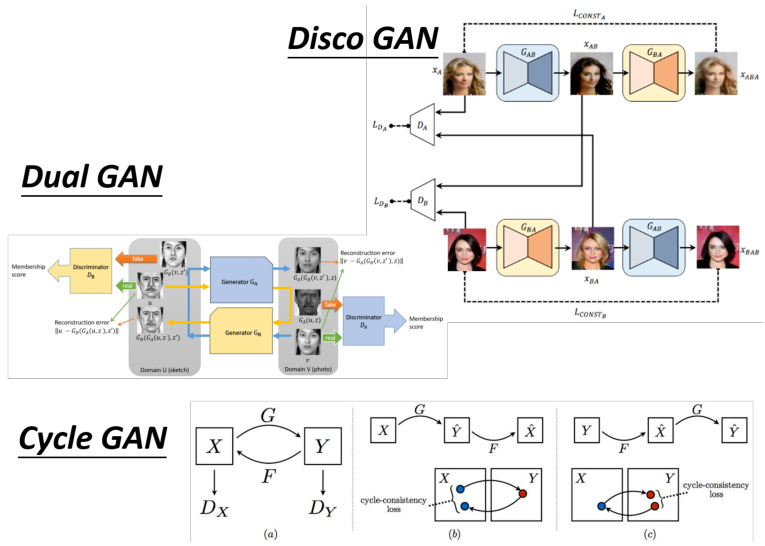
图 8.33 其他可以做风格转换的 GAN

除了 Cycle GAN 以外，还有很多其他的可以做风格转换的 GAN，比如 Disco GAN、DualGAN 等等，如图 8.33 所示。这些 GAN 的架构都是类似的，一样的想法。此外还有另外一个更进阶的可以做图像风格转换的版本，叫做 StarGAN。Cycle GAN 只能在两种风格间做转换，那 StarGAN 厉害的地方是它可以在多种风格间做转换。这些文章就等待大家去自己研究。

同样的 GAN 的应用不仅限于图像风格的转换，你也可以做文字风格的转换。比如说，把一句负面的句子转成正面的句子，这个也是可以用 GAN 来做的，只是输入变成文字，输出也变成文字而已。也就等于是输入一个序列，输出一个序列，这里可能会使用 Transformer 架构来做这个文字风格转换的问题。那具体怎么做文字的风格转换呢？其实和 Cycle GAN 是一模一样的。首先要有训练数据，收集一些负面的句子和一些正面的句子，可以从网络上直接爬虫得到。接下来就完全套用 Cycle GAN 的方法，假设我们是要负面的句子转正面的句子，那么判别器就要看现在生成器的输出像不像是真正的正面的句子。然后我们还要有另外一个生成器要学会把正面的句子转回原来负面的句子，要用 Cycle 的一致性。负面的句子转成正面的以后还可以转回原来负面的句子。两个句子的相似度也可以编码为向量来计算。

其实像这种文字风格转换还有很多其他的应用，不是只有正面句子转负面句子。举例来说，有很多长的文章想让机器学习文字风格的转换，让机器学会把长的文章变成简短的摘要。让它学会怎么精简的写作，让它学会把长的文章变成短的句子。另外，同样的想法可以做无监督的翻译，例如收集一堆英文的句子，同时收集一堆中文的句子，没有任何成对的数据，用Cycle GAN 硬做，机器就可以学会把中文翻成英文了。另外还有，无监督式的语音识别，也就是让机器听一些声音，然后学会把声音转成文字。这个也是可以用 Cycle GAN 来做的，只是输入变成声音，输出变成文字而已。当然还有很多很多的有趣的应用等待大家去探索。

这一节有关 GAN 的内容就介绍完了，主要为大家介绍了生成式模型、GAN、GAN 的理论、GAN 的训练小技巧、评估 GAN 的方法、条件型 GAN 以及 Cycle GAN 这种不需要数据对的 GAN 网络。如果大家想继续深入研究 GAN 的理论和应用，可以多去看一些综述类型的文章以及最新的论文。