第 2 章 实践方法论

在应用机器学习算法时，实践方法论能够帮助我们更好地训练模型。如果在 Kaggle 上的结果不太好，虽然 Kaggle 上呈现的是测试数据的结果，但要先检查训练数据的损失。看看模型在训练数据上面，有没有学起来，再去看测试的结果，如果训练数据的损失很大，显然它在训练集上面也没有训练好。接下来再分析一下在训练集上面没有学好的原因。

2.1 模型偏差

模型偏差可能会影响模型训练。举个例子，假设模型过于简单，一个有未知参数的函数代$\theta {\theta }_1$ 得到一个函数 $f_{{\mathit{\theta }}_1}(\mathit{x})$ ，同理可得到另一个函数 $f_{{\theta }_2}(xx)$ ，把所有的函数集合起来得到一个函数的集合。但是该函数的集合太小了，没有包含任何一个函数，可以让损失变低的函数不在模型可以描述的范围内。在这种情况下，就算找出了一个 ${\theta }^{\ast }$ ，虽然它是这些蓝色的函数里面最好的一个，但损失还是不够低。这种情况就是想要在大海里面捞针（一个损失低的函数），结果针根本就不在海里。

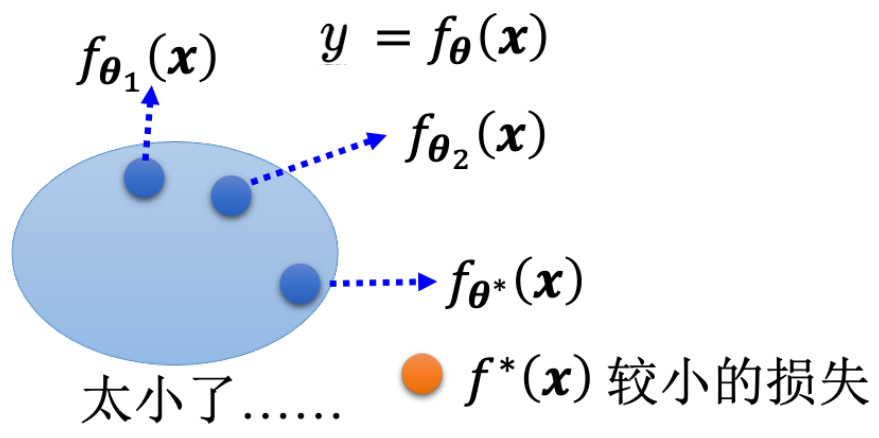
图 2.1 模型太简单的问题

这个时候重新设计一个模型，给模型更大的灵活性。以第一章的预测未来观看人数为例，可以增加输入的特征，本来输入的特征只有前一天的信息，假设要预测接下来的观看人数，用前一天的信息不够多，用 56 天前的信息，模型的灵活性就比较大了。也可以用深度学习，增加更多的灵活性。所以如果模型的灵活性不够大，可以增加更多特征，可以设一个更大的模型，可以用深度学习来增加模型的灵活性，这是第一个可以的解法。但是并不是训练的时候，损失大就代表一定是模型偏差，可能会遇到另外一个问题：优化做得不好。

2.2 优化问题

一般只会用到梯度下降进行优化，这种优化的方法很多的问题。比如可能会卡在局部最小值的地方，无法找到一个真的可以让损失很低的参数，如图 2.3(a) 所示。如图 2.3(b) 所示蓝色部分是模型可以表示的函数所形成的集合，可以把 $\theta \theta$ 代入不同的数值，形成不同的函数，把所有的函数通通集合在一起，得到这个蓝色的集合。这个蓝色的集合里面，确实包含了一些函数，这些函数它的损失是低的。但问题是梯度下降这一个算法无法找出损失低的函数，梯度下降是解一个优化的问题，找到 ${\theta }^{\ast }$ 就结束了。但 ${\theta }^{\ast }$ 的损失不够低。这个模型里面存在着某一个函数的损失是够低的，梯度下降没有给这一个函数。这就像是想大海捞针，针确实在海里，但是无法把针捞起来。训练数据的损失不够低的时候，到底是模型偏差，还是优化的问题呢。找不到一个损失低的函数，到底是因为模型的灵活性不够，海里面没有针。还是模型的灵活性已经够了，只是优化梯度下降不给力，它没办法把针捞出来 到底是哪一个。到底模型已经够大了，还是它不够大，怎么判断这件事呢？

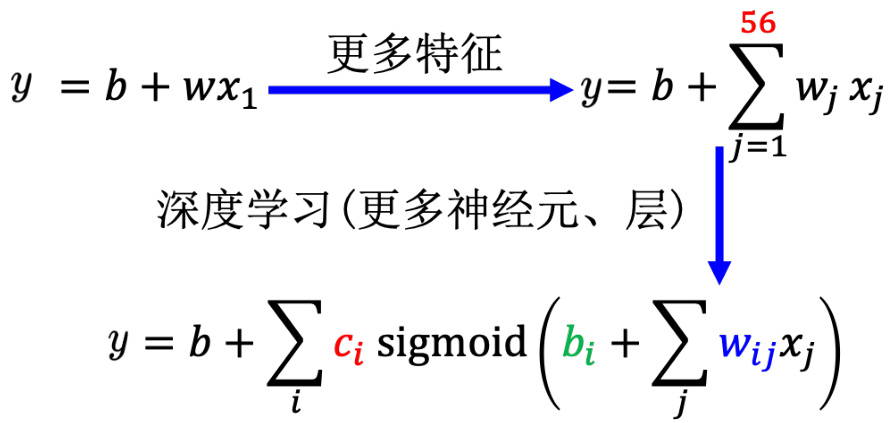
图 2.2 增加模型的灵活性

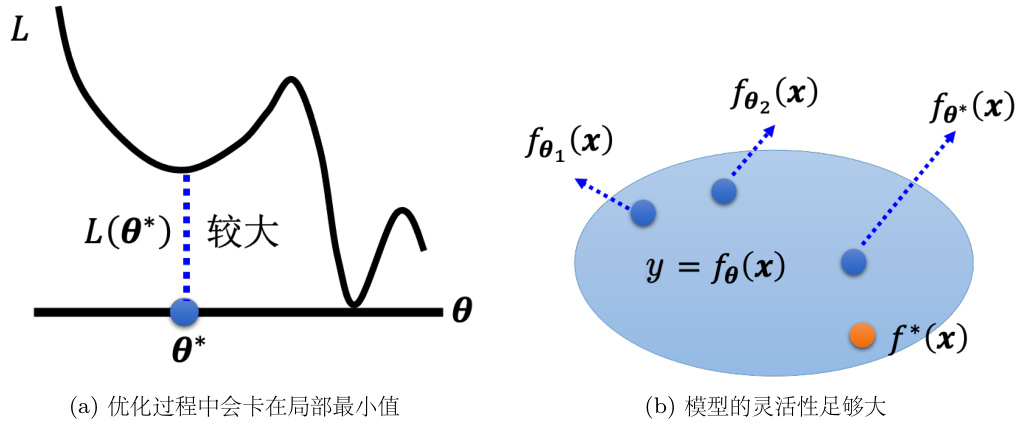
图 2.3 优化方法的问题

一个建议判断的方法，通过比较不同的模型来判断模型现在到底够不够大。举个例子，这一个实验是从残差网络的论文“Deep Residual Learning for Image Recognition”[1] 里面节录出来的。这篇论文在测试集上测试两个网络，一个网络有 20 层，一个网络有 56 层。图 2.4(a)横轴指的是训练的过程，就是参数更新的过程，随着参数的更新，损失会越来越低，但是结果20 层的损失比较低，56 层的损失还比较高。残差网络是比较早期的论文，2015 年的论文。很多人看到这张图认为这个代表过拟合，深度学习不奏效，56 层太深了不奏效，根本就不需要这么深。但这并非是过拟合，并不是所有的结果不好，都叫做过拟合。在训练集上，20 层的网络损失其实是比较低的，56 层的网络损失是比较高的，如图 2.4(b) 所示，这代表 56 层的网络的优化没有做好，它的优化不给力。

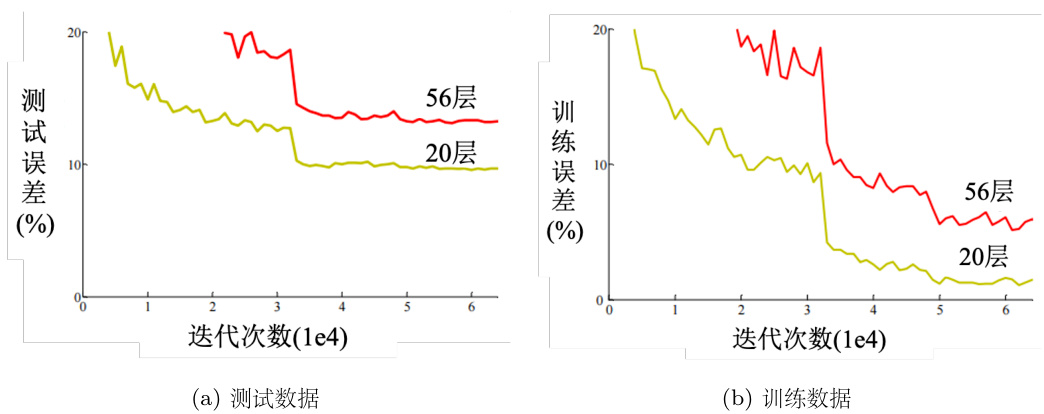
图 2.4 残差网络的例子

Q：如何知道是 56 层的优化不给力，搞不好是模型偏差，搞不好是 56 层的网络的模型灵活性还不够大，它要 156 层才好，56 层也许灵活性还不够大？

A：但是比较 56 层跟 20 层，20 层的损失都已经可以做到这样了，56 层的灵活性一定比 20 层更大。如果 56 层的网络要做到 20 层的网络可以做到的事情，对它来说是轻而易举的。它只要前 20 层的参数，跟这个 20 层的网络一样，剩下 36 层就什么事都不做，复制前一层的输出就好了。如果优化成功，56 层的网络应该要比 20 层的网络可以得到更低的损失。但结果在训练集上面没有，这个不是过拟合，这个也不是模型偏差，因为 56 层网络灵活性是够的，这个问题是优化不给力，优化做得不够好。

这边给大家的建议是看到一个从来没有做过的问题，可以先跑一些比较小的、比较浅的网络,或甚至用一些非深度学习的方法,比如线性模型、支持向量机(Support Vector Machine,SVM），SVM 可能是比较容易做优化的，它们比较不会有优化失败的问题。也就是这些模型它会竭尽全力的，在它们的能力范围之内，找出一组最好的参数，它们比较不会有失败的问题。因此可以先训练一些比较浅的模型，或者是一些比较简单的模型，先知道这些简单的模型，到底可以得到什么样的损失。

接下来还缺一个深的模型，如果深的模型跟浅的模型比起来，深的模型明明灵活性比较大，但损失却没有办法比浅的模型压得更低代表说优化有问题，梯度下降不给力，因此要有一些其它的方法来更好地进行优化。

举个观看人数预测的例子，如图 2.5 所示，在训练集上面，2017 年到 2020 年的数据是训练集，1 层的网络的损失是 280，2 层就降到 180，3 层就降到 140，4 层就降到 100。但是测 5 层的时候结果变成 340。损失很大显然不是模型偏差的问题，因为 4 层都可以做到 100了，5 层应该可以做得更低。这个是优化的问题，优化做得不好才会导致造成这样子的问题。如果训练损失大，可以先判断是模型偏差还是优化。如果是模型偏差，就把模型变大。假设经过努力可以让训练数据的损失变小，接下来可以来看测试数据损失；如果测试数据损失也小，比这个较强的基线模型还要小，就结束了。

但如果训练数据上面的损失小，测试数据上的损失大，可能是真的过拟合。在测试上的结果不好，不一定是过拟合。要把训练数据损失记下来，先确定优化没有问题，模型够大了。接下来才看看是不是测试的问题，如果是训练损失小，测试损失大，这个有可能是过拟合。

	1层	2层	3层	4层	5层
2017-2020	280	180	140	100	340

2.3 过拟合

为什么会有过拟合这样的情况呢？举一个极端的例子，这是训练集。假设根据这些训练集，某一个很废的机器学习的方法找出了一个一无是处的函数。这个一无是处的函数，只要输入 $x$ 有出现在训练集里面，就把它对应的 $y$ 当做输出。如果 $x$ 没有出现在训练集里面，就输出一个随机的值。这个函数啥事也没有干，其是一个一无是处的函数，但它在训练数据上的损失是 0。把训练数据通通丢进这个函数里面，它的输出跟训练集的标签是一模一样的，所以在训练数据上面，这个函数的损失可是 0 呢，可是在测试数据上面，它的损失会变得很大，因为它其实什么都没有预测，这是一个比较极端的例子，在一般的情况下，也有可能发生类似的事情。

如图 2.6 所示，举例来说，假设输入的特征为 $x$ ，输出为 $y$ ， $x$ 和 $y$ 都是一维的。 $x$ 和 $y$ 之间的关系是 2 次的曲线，曲线用虚线来表示，因为通常没有办法，直接观察到这条曲线。我们真正可以观察到的是训练集，训练集可以想像成从这条曲线上面，随机采样出来的几个点。模型的能力非常的强，其灵活性很大，只给它这 3 个点。在这 3 个点上面，要让损失低，所以模型的这个曲线会通过这 3 个点，但是其它没有训练集做为限制的地方，因为它的灵活性很大，所以模型可以变成各式各样的函数，没有给它数据做为训练，可以产生各式各样奇怪的结果。

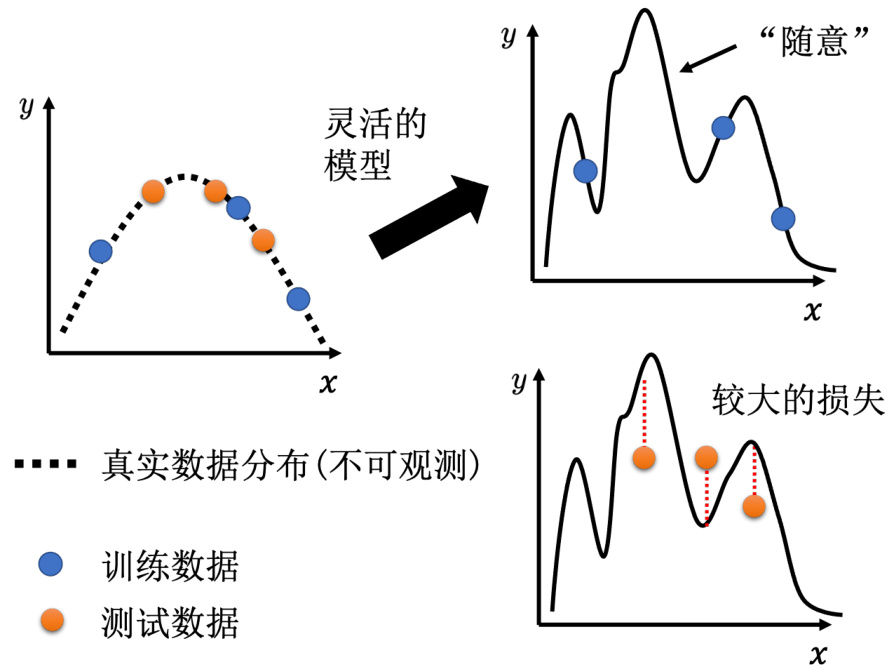
图 2.5 层数越深，损失反而变大
图 2.6 模型灵活导致的问题

如果再丢进测试数据，测试数据和训练数据，当然不会一模一样，它们可能是从同一个分布采样出来的，测试数据是橙色的点，训练数据是蓝色的点。用蓝色的点，找出一个函数以后，测试在橘色的点上，不一定会好。如果模型它的自由度很大的话，它可以产生非常奇怪的曲线，导致训练集上的结果好，但是测试集上的损失很大。

怎么解决过拟合的问题呢，有两个可能的方向：

第一个方向是往往是最有效的方向，即增加训练集。因此如果训练集，蓝色的点变多了，虽然模型它的灵活性可能很大，但是因为点非常多，它就可以限制住，它看起来的形状还是会很像，产生这些数据背后的 2 次曲线，如图 2.7 所示。可以做数据增强（data augmentation，），这个方法并不算是使用了额外的数据。

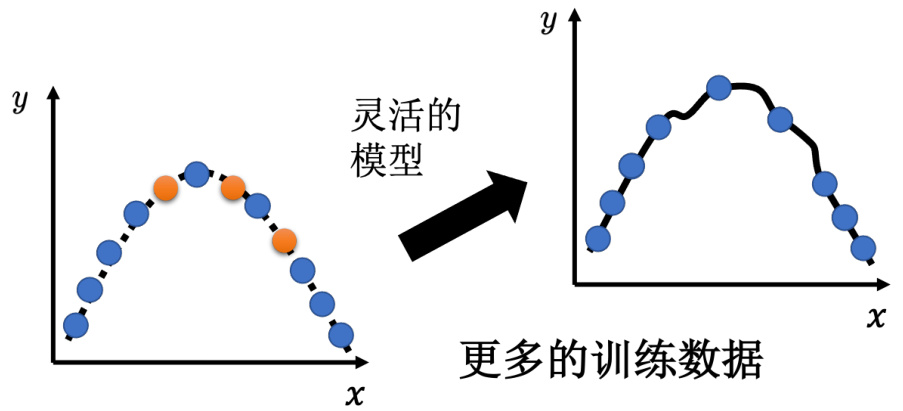
图 2.7 增加数据

数据增强就是根据问题的理解创造出新的数据。举个例子，在做图像识别的时候，常做的一个招式是，假设训练集里面有某一张图片，把它左右翻转，或者是把它其中一块截出来放大等等。对图片进行左右翻转，数据就变成两倍。但是数据增强不能够随便乱做。在图像识别里面，很少看到有人把图像上下颠倒当作增强。因为这些图片都是合理的图片，左右翻转图片，并不会影响到里面的内容。但把图像上下颠倒，可能不是一个训练集或真实世界里面会出现的图像。如果给机器根据奇怪的图像学习，它可能就会学到奇怪的东西。所以数据增强，要根据对数据的特性以及要处理的问题的理解，来选择合适的数据增强的方式。

另外一个解法是给模型一些限制，让模型不要有过大的灵活性。假设 $x$ 跟 $y$ 背后的关系其实就是一条 2 次曲线，只是该 2 次曲线里面的参数是未知的。如图 2.8 所示，要用多限制的模型才会好取决于对这个问题的理解。因为这种模型是自己设计的，设计出不同的模型，结果不同。假设模型是 2 次曲线，在选择函数的时候有很大的限制，因为 2 次曲线要就是这样子，来来去去就是几个形状而已。所以当训练集有限的时候，来来去去只能够选几个函数。所以虽然说只给了 3 个点，但是因为能选择的函数有限，可能就会正好选到跟真正的分布比较接近的函数，在测试集上得到比较好的结果。

解决过拟合的问题，要给模型一些限制，最好模型正好跟背后产生数据的过程，过程是一样的就有机会得到好的结果。给模型制造限制可以有如下方法：

• 给模型比较少的参数。如果是深度学习的话，就给它比较少的神经元的数量，本来每层一千个神经元，改成一百个神经元之类的，或者让模型共用参数，可以让一些参数有一样的数值。全连接网络（fully-connected network）其实是一个比较有灵活性的架构，而卷积神经网络（Convolutional Neural Network，CNN）是一个比较有限制的架构。CNN 是一种比较没有灵活性的模型，其是针对图像的特性来限制模型的灵活性。所以全连接神经网络，可以找出来的函数所形成的集合其实是比较大的，CNN 所找出来的函数，它形成的集合其实是比较小的，其实包含在全连接网络里面的，但是就是因为CNN 给了，比较大的限制，所以 CNN 在图像上，反而会做得比较好，这个之后都还会

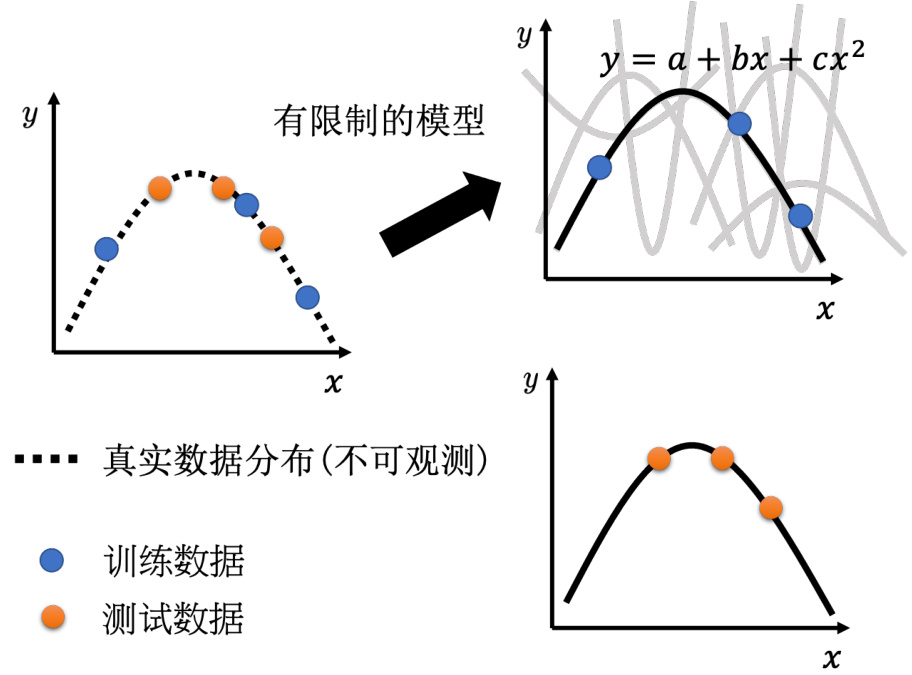
图 2.8 对模型增加限制

再提到，

• 用比较少的特征，本来给 3 天的数据，改成用给两天的数据，其实结果就好了一些。

·还有别的方法,比如早停(early stopping)正则化(regularization)和丢弃法(dropoutmethod）。

但也不要给太多的限制。假设模型是线性的模型，图 2.9 中有 3 个点，没有任何一条直线可以同时通过这 3 个点。只能找到一条直线，这条直线跟这些点比起来，它们的距离是比较近的。这个时候模型的限制就太大了，在测试集上就不会得到好的结果。这种情况下的结果不好，并不是因为过拟合了，而是因为给模型太大的限制，大到有了模型偏差的问题。

这边产生了一个矛盾的情况，模型的复杂程度，或这样让模型的灵活性越来越大。但复杂的程度和灵活性都没有给明确的定义。比较复杂的模型包含的函数比较多，参数比较多。如图 2.10 所示，随着模型越来越复杂，训练损失可以越来越低，但测试时，当模型越来越复杂的时候，刚开始，测试损失会跟著下降，但是当复杂的程度，超过某一个程度以后，测试损失就会突然暴增了。这就是因为当模型越来越复杂的时候，复杂到某一个程度，过拟合的情况就会出现，所以在训练损失上面可以得到比较好的结果。在测试损失上面，会得到比较大的损失，可以选一个中庸的模型，不是太复杂的，也不是太简单的，刚刚好可以在训练集上损失最低，测试损失最低。

假设 3 个模型的复杂的程度不太一样，不知道要选哪一个模型才会刚刚好，在测试集上得到最好的结果。因为选太复杂的就过拟合，选太简单的有模型偏差的问题。把这 3 个模型的结果都跑出来，上传到 Kaggle 上面，损失最低的模型显然就是最好的模型，但是不建议这么做。举个极端的例子，假设有 1 到 ${10}^{12}$ 个模型，这些模型学习出来的函数都是一无是处的函数。它们会做的事情就是，训练集里面有的数据就把它记下来，训练集没看过的，就直接输出随机的结果。把这 ${10}^{12}$ 个模型的结果，通通上传到 Kaggle 上面，得到 ${10}^{12}$ 个分数，这${10}^{12}$ 的分数里面，结果最好的，模型也是最好的。

虽然每一个模型没看过测试数据，其输出的结果都是随机的，但不断随机，总是会找到一个好的结果。因此也许某个模型找出来的函数，正好在测试数据上面的结果比较好，选这一个模型当作最后上传的结果，当作最后要用在私人测试集上的结果。该模型是随机的，它恰好在公开的测试数据上面得到一个好结果，但是它在私人测试集上可能仍然是随机的。测试集分成公开的数据集跟私人的数据集，公开的分数可以看到，私人的分数要截止日期以后才知道。如果根据公开数据集来选择模型，可能会出现这种情况：在公开的排行榜上面排前十，但是截止日期一结束，可能掉到 300 名之外。因为计算分数的时候，会同时考虑公开和私人的分数。

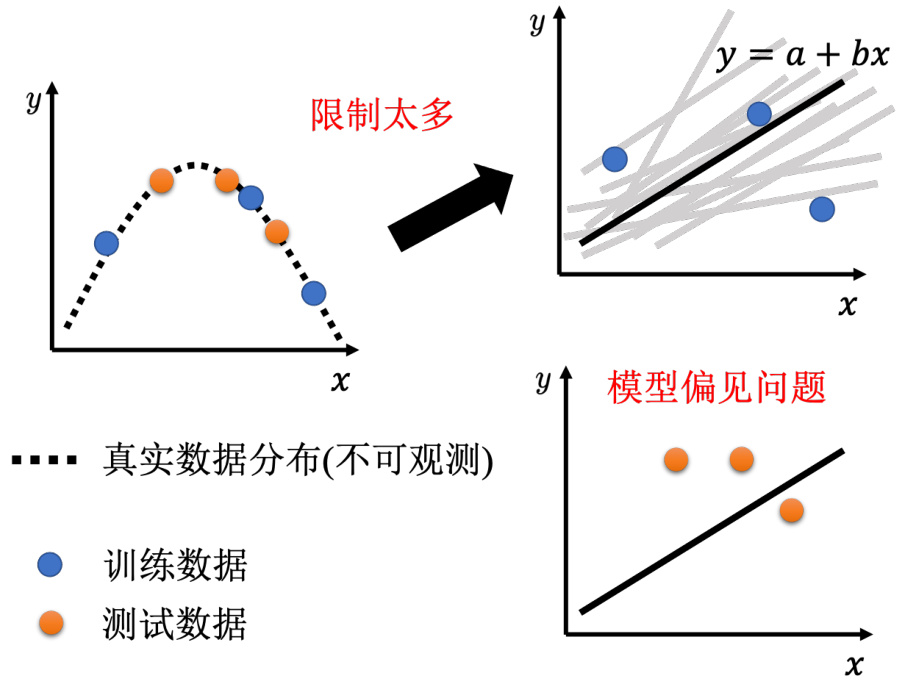
图 2.9 限制太大会导致模型偏差

Q：为什么要把测试集分成公开和私人？

A：假设所有的数据都是公开，就算是一个一无是处的模型，它也有可能在公开的数据上面得到好的结果。如果只有公开的测试集，没有私人测试集，写一个程序不断随机产生输出就好，不断把随机的输出上传到 Kaggle，可以随机出一个好的结果。这个显然没有意义。而且如果公开的测试数据是公开的，公开的测试数据的结果是已知的，一个很废的模型也可能得到非常好的结果。不要用公开的测试集调模型，因为可能会在私人测试集上面得到很差的结果，不过因为在公开测试集上面的好的结果也有算分数。

2.4 交叉验证

比较合理选择模型的方法是把训练的数据分成两半，一部分称为训练集（training set），一部分是验证集（validation set）。比如 $90\mathrm{\%}$ 的数据作为训练集，有 $10\mathrm{\%}$ 的数据作为验证集。在训练集上训练出来的模型会使用验证集来衡量它们的分数，根据验证集上面的分数去挑选结果，再把这个结果上传到 Kaggle 上面得到的公开分数。在挑分数的时候，是用验证集来挑模型，所以公开测试集分数就可以反映私人测试集的分数。但假设这个循环做太多次，根据公开测试集上的结果调整模型太多次，就又有可能在公开测试集上面过拟合，在私人测试集上面得到差的结果。不过上传的次数有限制，所以无法走太多次循环，可以避免在公开的测试集上面的结果过拟合。根据过去的经验，就在公开排行榜上排前几名的，往往私人测试集很容易就不好。

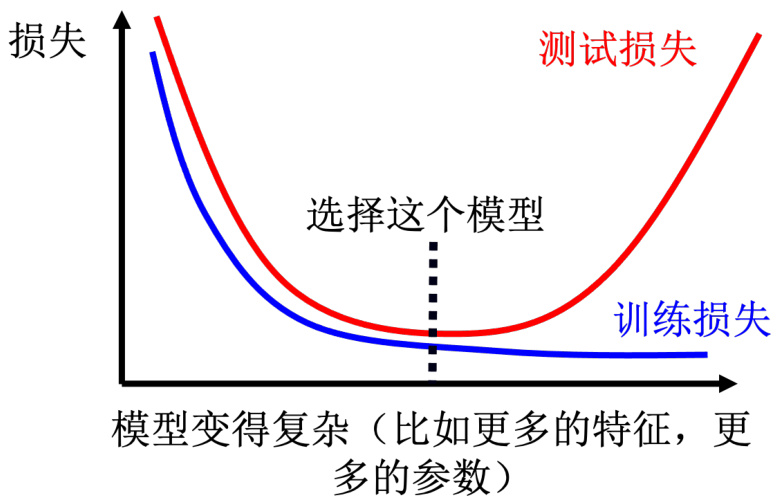
图 2.10 模型的复杂程度与损失的关系

其实最好的做法，就是用验证损失，最小的直接挑就好了，不要管公开测试集的结果。在实现上，不太可能这么做，因为公开数据集的结果对模型的选择，可能还是会有些影响的。理想上就用验证集挑就好，有过比较好的基线（baseline）算法以后，就不要再去动它了，就可以避免在测试集上面过拟合。但是这边会有一个问题，如果随机分验证集，可能会分得不好，分到很奇怪的验证集，会导致结果很差，如果有这个担心的话，可以用 $k$ 折交叉验证（ $k$ -foldcross validation），如图 2.11 所示。 $k$ 折交叉验证就是先把训练集切成 $k$ 等份。在这个例子，训练集被切成 3 等份，切完以后，拿其中一份当作验证集，另外两份当训练集，这件事情要重复 3 次。即第一份第 2 份当训练，第 3 份当验证；第一份第 3 份当训练，第 2 份当验证；第一份当验证，第 2 份第 3 份当训练。

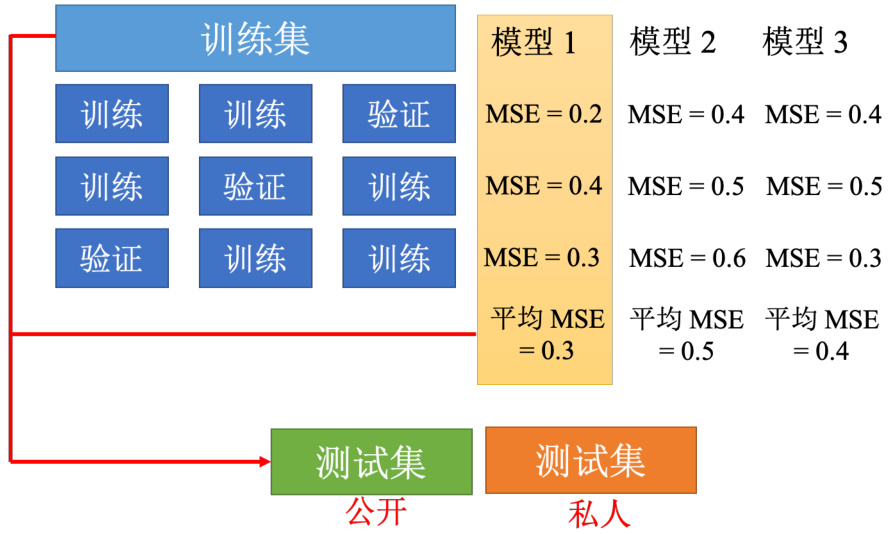
图 2.11 k 折交叉验证

接下来有 3 个模型，不知道哪一个是好的。把这 3 个模型，在这 3 个设置下，在这 3 个训练跟验证的数据集上面，通通跑过一次，把这 3 个模型，在这 3 种情况的结果都平均起来，把每一个模型在这 3 种情况的结果，都平均起来，再看看谁的结果最好假设现在模型 1 的结果最好，3 折交叉验证得出来的结果是，模型 1 最好。再把模型 1 用在全部的训练集上，训练出来的模型再用在测试集上面。接下来也许我们要问的一个问题是，讲到预测 2 月 26 日，也就是上周五的观看人数的结果如图 2.12 所示。所以把 3 层的网络，拿来测试一下是测试的结果。

图 2.12 3 层网络的结果最好

2.5 不匹配

图 2.13 中横轴就是从 2021 年的 1 月 1 号开始一直往下，红色的线是真实的数字，蓝色的线是预测的结果。2 月 26 日是 2021 年观看人数最高的一天了，机器的预测差距非常的大，差距有 2580，所以这一天是 2021 年观看人数最多的一天。跑了一层 2 层跟四层的看看，所有的模型的结果都不好，两层跟 3 层的错误率都是 2 千多，其实四层跟一层比较好，都是 1800左右，但是这四个模型不约而同的，觉得 2 月 26 日应该是个低点，但实际上 2 月 26 日是一个峰值，模型其实会觉得它是一个低点，也不能怪它，因为根据过去的数据，周五晚上大家都出去玩了。但是 2 月 26 日出现了反常的情况。这种情况应该算是另外一种错误的形式，这种错误的形式称为不匹配（mismatch）。

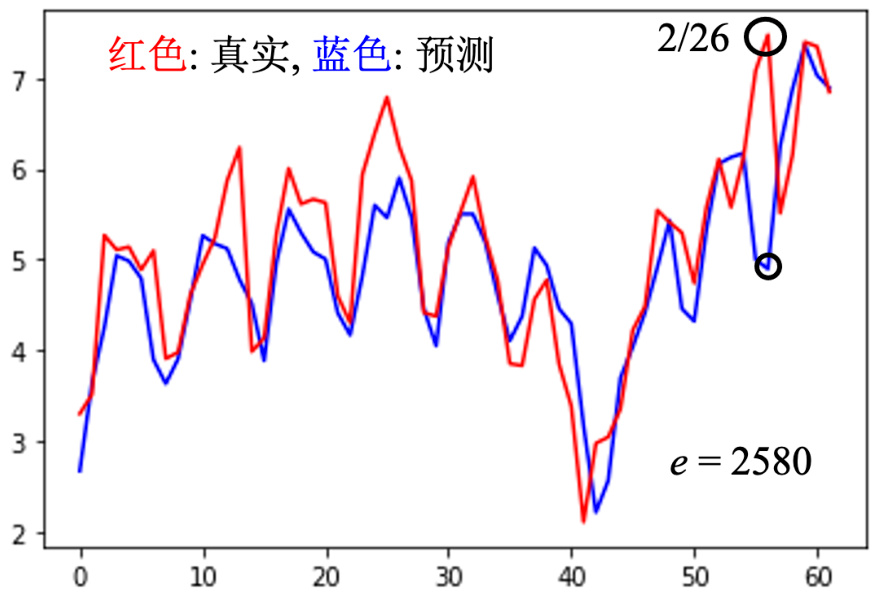
图 2.13 另一种错误形式：不匹配

不匹配跟过拟合其实不同，一般的过拟合可以用搜集更多的数据来克服，但是不匹配是指训练集跟测试集的分布不同，训练集再增加其实也没有帮助了。假设数据在分训练集跟测试集的时候，使用 2020 年的数据作为训练集，使用 2021 年的数据作为测试集，不匹配的问题可能就很严重。如果今天用 2020 年当训练集，2021 年当测试集，根本预测不准。因为 2020年的数据跟 2021 年的数据背后的分布不同。图 2.14 是图像分类中的不匹配问题。增加数据也不能让模型做得更好，所以这种问题要怎么解决，匹不匹配要看对数据本身的理解了，我们可能要对训练集跟测试集的产生方式有一些理解，才能判断它是不是遇到了不匹配的情况。

图 2.14 图像分类的不匹配问题

参考文献

[1] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]// Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.