第 17 章 网络压缩

网络压缩（network compression）是一个很重要的方向，Bert 或 GPT 之类的模型很大，能不能够把这些硕大无朋的模型它缩小，能不能够简化这些模型，让它有比较少量的参数，但是跟原来的性能其实是差不多的呢，这就是网络压缩想要做的事情。很多时候，需要把这些模型用在资源受限的环境下。有时候我们会需要把这些机器学习的模型。举个例子，跑在智能手表，这些边缘设备（edge device）只有比较少的内存，只有比较少的计算力。模型如果太过巨大，手表可能会是跑不动的，所以会需要比较小的模型。

Q：为什么会需要在这些边缘设备上面跑模型呢？为什么不把数据传到云端，直接在云端上做计算，再把结果传回到边缘设备？

A：以手表为例，为什么一定要在手表上面做计算呢？一个常见的理由是延迟的问题。假设需要把数据传到云端，云端计算完再传回来，那中间就会有一个时间差。假设边缘设备是自驾车的一个传感器，也许自驾车的传感器需要做非常即时的回应，需要把数据传到云端再传回来，中间的延迟太长了，也许会长到是不能接受的。虽然在未来 5G的时代延迟可能可以忽略不计，但需要在边缘设备上面做计算的理由，这个理由就是隐私。如果需要把数据传到云端，云端的系统持有者不就看到我们的数据了。因此为了保障隐私，也许在智能手表上直接进行计算并进行决策是一个可以保障隐私的做法。

接下来介绍五个以软件为导向的网络压缩技术，这些技术只是在软件上面对网络进行压缩，都不考虑硬件加速的部分。

17.1 网络剪枝

第一个技术是网络剪枝（network pruning)。网络剪枝就是要把网络里面的一些参数剪掉。剪枝就是修剪的意思，把网络里面的一些参数剪掉。为什么可以把网络里面的一些参数剪掉呢？这么大的网络里面有很多很多的参数，每一个参数不一定都有在做事。参数这么多的时候，也许很多参数只是在划水，什么事也没有做。这些没有做的参数放在那边，就只是占空间而已，浪费计算资源而已。为何就把它们剪掉呢？所以网络剪枝就是把一个大的网络中没有用的那些参数把它找出来，把它扔掉。人刚出生的时候，脑袋是空空的，神经元跟神经元间没什么连接。在六岁的时候会长出非常多的连接。但是随着年龄渐长，有一些连接就慢慢消失了。这个跟网络剪枝有异曲同工之妙。网络剪枝不是太新的概念，早在这个 90 年代，YannLe Cun 的论文“Optimal Brain Damage”是讲网络剪枝，他把大脑（网络）剪枝，把它剪掉一些权重看成是一种脑损伤，最优的意思是要找出最好的剪枝的方法，让一些权重被剪掉之后，但是对这个脑的损伤是最小的。

网络剪枝其框架如图 17.1 所示，首先，先训练一个大的网络。接下来去衡量这个大的网络里面每一个参数或者是每一个神经元的重要性，去评估一下有没有哪些参数是没在做事的，或有没有哪些神经元是没在做事的。怎么评估某一个参数有没有在做事呢，怎么评估某一个参数重不重要呢。最简单的方法也许就是看它的绝对值。如果这个参数的绝对值越大，它可能越能对整个网络的影响越大。或者如果它的绝对值越接近零。也许对整个网络的影响越小，也许对我们任务的影响越小。

我们可以评估每一个神经元的重要性，把神经元当作修剪的单位。怎么看一个神经元重不重要呢？比如计算这个神经元输出不为零的次数等等。总之有非常多的方法来判断一个参数或一个神经元是否重要。把不重要的神经元或是不重要的参数就剪掉，就把它从模型里面移出，就得到一个比较小的网络。但是做完这个修剪以后，通常模型的性能就会掉一点。因为有一些参数被拿掉了。所以这个网络当然是受到一些损伤，正确率就掉一点。但是我们会想办法让这个正确率再回升一点。可以把这个比较小的网络，把剩余没有被剪掉的参数，再重新做微调。把训练数据拿出来，把这个比较小的网络再重新训练一下。训练完之后，其实还可以重新再去评估一次每一个参数的正确性，还可以再去除掉，再剪掉更多的参数，再重新进行微调，这个步骤可以反复进行多次。

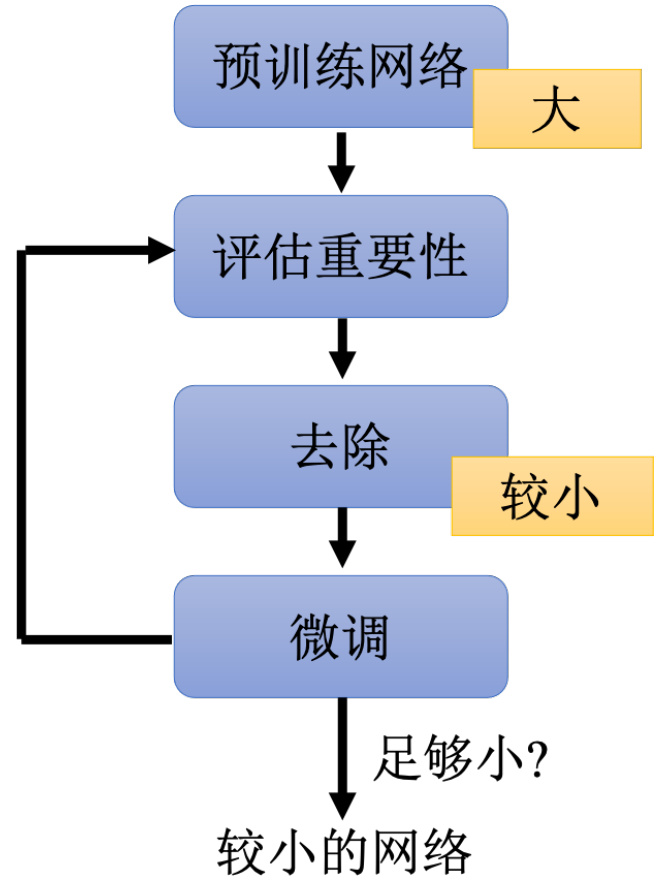
图 17.1 剪枝框架

为什么不一次剪掉大量的参数，因为在实验上，如果一次剪掉大量的参数，可能对网络的伤害太大了，可能会大到用微调也没有办法复原。所以一次先剪掉一点参数。比如说只剪掉$10\mathrm{\%}$ 的参数，然后再重新训练，然后再重新剪掉 $10\mathrm{\%}$ 的参数，再重新训练，反复这一个过程。我们可以剪掉比较多的参数，当网络够小以后，整个过程就完成了，就得到一个比较小的网络。而且这个比较小的网络，也许它的正确率跟大的网络是没有太大的差别的。修剪的单位可以以参数为单位，也可以以神经元来当作单位，这两者作为单位，在实现上会是有显著不同。如果我们现在是以参数当作单位会发生什么事，假设我们是要评估某一个参数要不要被去掉，某个参数对整个任务而言重不重要能不能够被去掉，我们把这个不重要的参数去掉以后，得到的网络的形状可能会是不规则的。如图 17.2 所示，所谓不规则的意思是说，举例来说，红色的这个神经元连到接下来三个绿色的神经元，但第二个红色的神经元只连到两个绿色的神经元。或这个红色的神经元的输入只有两个蓝色的神经元，而这个红色的神经元的输入有四个蓝色的神经元。如果把参数当作单位来进行修剪的话，修剪完以后的网络的形状会是不规

则的。

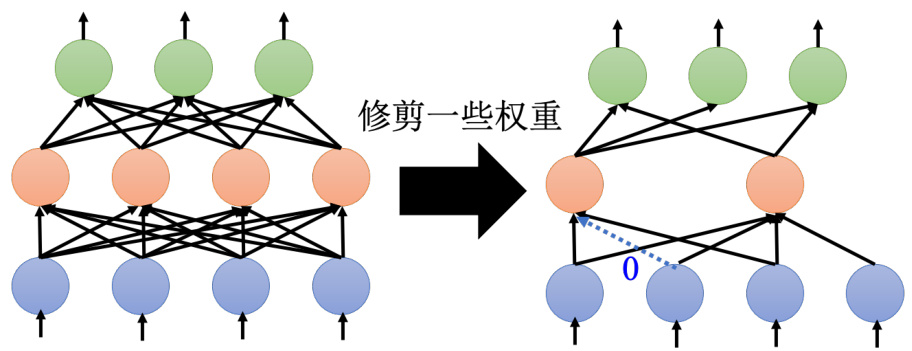
图 17.2 剪枝的问题

形状不规则最大的问题就是不好实现。用 PyTorch 要实现这种形状不规则的网络，不好实现。因为在 PyTorch 里面，定义第一个网络的时候，定义方法都是每一层有几个神经元，定义现在每一层要输入几个输入，输入有几个神经元，输出有几个神经元。或者输入多长的向量，输出有多长的向量。这种形状不固定的网络根本不好实现，而且就算硬是把这种形状不规则的网络实现出来，用 GPU 也很难加速。GPU 在加速的时候，就是把网络的计算看成一个矩阵的乘法，但是当网络是不规则的时候，不容易用矩阵的乘法来进行加速，我们不容易用GPU 来进行加速，所以实际在做权重剪枝的时候，在实现上我们可能会把那些修剪掉的权重直接补零，就是修剪掉的权重不是不存在，它的值只是设为零。这样的好处是实现就比较容易，比较容易用 GPU 加速，但根本就没有真的把网络变小，虽然权重值是零，但还是存了这个参数，我们还是存了一个参数在内存里面，并没有真的把网络变小。这是以参数为单位来做剪枝的时候，实现上会遇到的问题。

如图 17.3 所示，紫色的这一条线是指稀疏程度（sparsity）。稀疏程度就是有多少百分比的参数现在被修剪掉了。紫色的这条线的值都很接近 1，代表有接近大概 $95\mathrm{\%}$ 以上的参数都被修剪掉了。网络剪枝其实是一个非常有效率的方法，往往可以修剪到 $95\mathrm{\%}$ 以上的参数，但是准确率只掉 $12\mathrm{\%}$ 而已。所以这边参数修剪时，有 $95\mathrm{\%}$ 的参数都被丢掉了，只剩下 $5\mathrm{\%}$ 的参数，这个网络变得很小，的计算要很快吧。但实际上我们发现根本就没有加速多少，甚至可以说根本就没有加速。图 17.3 中的长条图显示的是在三种不同的计算资源上面，加速的程度。加速的程度要大过 1 才有加速，加速程度小于 1 其实是变慢的。在多数情况下根本就没有加速，多数情况下其实都是变慢，也就是把一些权重修剪掉，结果网络形状变得不规则，真的用GPU 加速的时候，反而没有办法真的加速它，所以权重剪枝不一定是一个特别有效的方法。

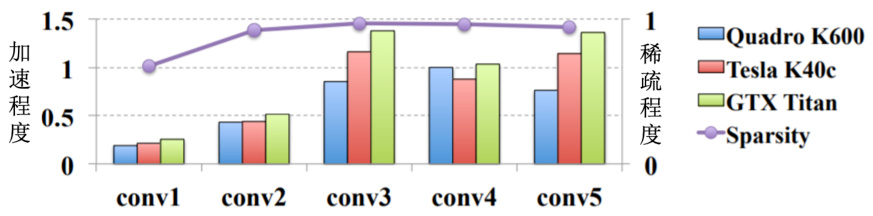
图 17.3 权重剪枝无法用 GPU 加速[1]

神经元剪枝，即以神经元为单位来做剪枝也许是一个比较有效的方法。如果用神经元做单位来剪枝，丢掉一些神经元以后，网络的架构仍然是规则的。这种用 PyTorch 也比较好实现，实现的时候，只要改那个每一个层输入、输出的那个维度就好了，也比较好用 GPU 来加速。

接下来要问一个问题：我们先训练一个大的网络，再把它变小，而且说小的网络跟大的网络的正确率没有差太多。不直接训练一个小的网络就好了，直接训练一个小的网络比较有效率，还训练大的网络变小干嘛，根本是舍本逐末，为什么不直接训练小的网络？一个普遍的答案是大的网络比较好训练。如果直接训练一个小的网络，往往没有办法得到跟大的网络一样的正确率。我们可以先训练一个大的网络，再把它变小，正确率没有掉太多。但直接训练小的网络，得不到大的网络剪枝完变得小的网络一样的正确率。

为什么大的网络比较好训练？有一个假说叫做彩票假说（lottery ticket hypothesis）。假说代表说它不算是一个被实证的理论。但它现在只是一个假说而已，这个彩票假说是怎么解释为什么大的网络比较容易训练，直接训练一个小的网络没有办法得到跟大的网络一样的效果，一定要大的网络剪枝变小，结果才会好。彩票假说是这样说的，每次训练网络的结果不一定会一样。我们抽到一组好的初始的参数，就会得到好的结果；抽到一组坏初始的参数，就会得到坏的结果。但如何在彩票这个游戏里面得到比较高的中奖率，是不是就是包牌买比较多的彩券，可以增加中奖率，所以对一个大的网络来说也是一样的。大的网络可以视为是很多小的子网络（sub-network）的组合。如图 17.4 所示，我们可以想成是一个大的网络里面其实包含了很多小的网络。训练这个大的网络的时候，等于同时训练很多小的网络。每一个小的网络不一定可以成功的被训练出来。所谓成功的训练出来是说它不一定可以，通过梯度下降找到一个好的解，不一定可以训练出一个好的结果，不一定可以让它的损失变低。但是在众多的子网络里面，只要其中一个子网络成功，大的网络就成功了。而如果大的网络里面包含的小的网络越多，就好像是去买彩票的时候，买比较多的彩券一样，彩券越多，中奖的概率就越高。一个网络越大，它就越有可能成功的被训练起来。彩票假说在实验上是怎么被证实的？它在实验上的证实方式跟网络的剪枝非常有关系，所以直接看一下在实验上是怎么证实彩票假说的。

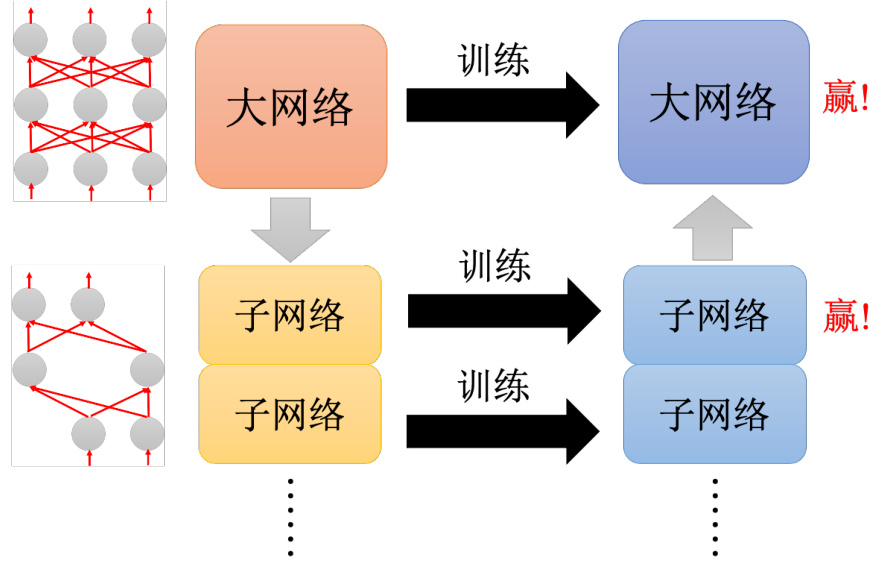
图 17.4 大网络包含了很多小网络

如图 17.5 所示，现在有一个大的网络，在这个大的网络上面一开始的参数是随机初始化。把参数随机初始化以后，得到一组训练完的参数。训练完的参数用紫色来表示，接下来用网络剪枝的技术，把一些紫色的参数丢掉，而得到一个比较小的网络。如果直接把这个小的网络里面的参数，再重新随机的去初始化，也就是重训练一个一样大小的小的网络，就是我们把这个网络复制一次。但是参数完全不一样，重新再训练一次。重新再训练一次，直接训练这个小的网络，训练不起来，训练一个大的再把它变小，没问题。但假设这一个小的网络，再重新初始化参数的时候，我们用的跟这组红色的参数是一模一样的，就训练得起来。

这两组参数虽然都是随机初始化的，但是这组绿色的参数跟这组红色的参数是没有关系的。而这边这些随机初始化的参数是直接从这边的红色参数里面选出对应的参数，就是这边有四个参数。我们就是把这边对应到的这四个参数直接把它复制过来，这边有四个参数。我们就把这里面对应到的四个参数直接复制过来，把这里面的参数直接复制过来就训练了起来。如果用彩票假说来解释的话，就是这里面有很多子网络。而这一组初始化的参数，就是幸运的那一组可以训练得起来的子网络，所以用把这些网络，把这个大的网络训练完，再剪枝掉的时候，留下来的就是幸运的那些参数，可以训练得起来的那些参数，所以这一组初始化的参数是可以训练得起来的一个子网络。但是如果我们再重新随机初始化的话，就抽不到可以成功训练起来的参数，所以这个就是彩票假说。彩票假说非常地知名，它得到了 ICLR 2019 的最佳论文奖。

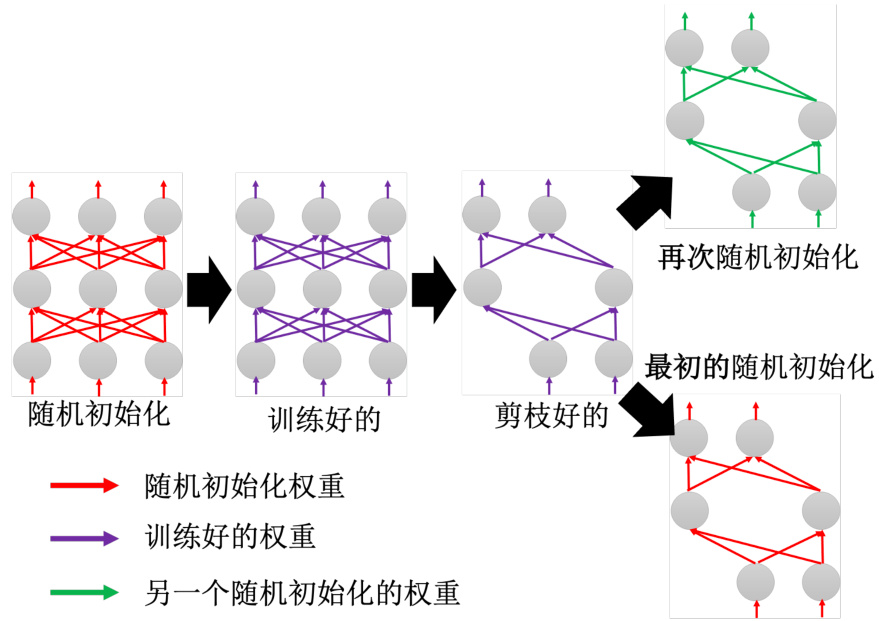
图 17.5 彩票假说

后面也有很多后续的研究，比如说有一篇有趣的研究叫做“Deconstructing Lottery Tick-ets: Zeros, Signs, and the Supermask”[2]。解构这个彩票有什么有趣的结论，直接讲它的结论。第一个试了不同的剪枝策略，它做了一个非常完整的实验发现说，如果训练前跟训练后权重绝对值差距越大，剪枝那些网络得到的结果是越有效的。另外一个比较有趣的结果是，到底这一组好的初始化是好在哪里呢？如果我们只要不改变参数的正负号，就可以训练起来，小的网络只要不改变正负号，就可以训练起来。假设剪枝完以后，剩下的这个数。假设剪枝完以后，再把原来随机初始化的那些参数拿出来，它的值是 $0.9,3.1,-9.1,8.5$ ，可以完全不管它的数值，直接把正的数值的通通都用 $+\alpha$ 来取代，小于 0 的都用 $-\alpha$ 来取代，即 $+\alpha ,+\alpha ,-\alpha ,+\alpha$ 。

用这组参数去初始化模型，这样也训练得起来，会跟用这组参数去初始化差不多。所以这个实验告诉我们说正负号是初始化参数，能不能够训练起来的关键，它的绝对值不重要，正负号才重要。

最后一个神奇的发现是，既然我们在想说一个大的网络里面有一些网络有一些子网络，它是特别是好的初始化的参数，它训练起来会特别地顺利。会不会一个大的网络里面甚至其实已经有一个子网络，它连训练都不用训练，直接拿出来就是一个好的网络呢？我们完全不用训练网络，直接把大的网络剪枝，就得到一个可以拿来做分类的分类器了，有没有可能是这个样子的呢。就好像米开朗基罗说：“塑像就在石头里，我只是把不需要的部分去掉”，会不会在整个大的网络里面，算参数都是随机的，其中已经有一组参数，它就已经可以做分类了，把多余的东西拿掉，直接就可以得到好的分类结果的。

但是彩票假说不一定是对的，论文“Rethinking the Value of Network Pruning”[3] 是打脸彩票假说，而且神奇的是这篇文章跟彩票假说是同时出来的，它们同时出现在 ICLR 2019，它们得到了不太一样的结论。这篇文章试了两个数据集，还有好几种不同的模型，这个是没有剪枝过的网络的正确率，然后它试着去剪枝了一下网络，再重新去做微调。小的网络可以跟大的网络得到差不多的正确率。然后它说一般人的想像是，如果直接去训练小的网络，正确率会不如大的网络剪枝完以后的结果。

其实在这篇文章里面也有对彩票假说做出一些回应，它觉得彩票假说观察到的现象，也许只有在某一些特定的情况下才观察得到。根据这篇文章的实验，只有在学习率设比较小的时候，还有非结构化的（unstructured）的时候，就是剪枝的时候是以权重作为单位来做剪枝的时候，才能观察到彩票假说的现象，它发现说学习率调大，它就观察不到彩票假说的这个现象，所以到底彩票假说的正确性尚待更多的研究来证实。

17.2 知识蒸馏

接下来讲可以让网络变小的方法——知识蒸馏（knowledge distillation）。先训练一个大的网络，这个大的网络在知识蒸馏里面称为教师网络（teacher network），其是老师。我们要训练的是真正想要的小的网络，即学生网络（student network）。先训练一个大的网络称为教师网络。再根据这个大的网络来制造学生网络。在网络剪枝里面，直接把那个大的网络做一些修剪，把大的网络里面一些参数拿掉，就把它变成小的网络。在知识蒸馏里面是不一样的，这个小的网络（学生网络）是去根据教师网络来学习。假设要做手写数字识别，就把训练数据都丢到教师里面，教师就产生输出，因为这是一个分类的问题，所以教师的输出其实是一个分布。

比如教师的输出可能是看到这张图片 1 的分数是 0.7，7 的分数是 0.2，9 这个数字的分数是 0.1 等等。接下来给学生一模一样的图片，但是学生不是去看这个图片的正确答案来学习，它把老师的输出就当做正确答案，也就是老师输出 1 要 0.7，7 要 0.2，9 要 0.1。学生的输出也就要尽量去逼近老师的输出，尽量去逼近 1 是 0.7、7 是 0.2、9 是 0.1 这样的答案。学生就是根据老师的答案学，就算老师的答案是错的，学生就去学一个错的东西。

Q：为什么不直接训练一个小的网络？为什么不直接把小的网络去根据正确答案学习，而是要多加一个步骤先让大的网络学，再用小的网络去跟大的网络学习呢？这边的理由跟网络剪枝是一样的。
A：直接训练一个小的网络，往往结果就是没有从大的网络剪枝好。知识蒸馏的概念是一样的，因为直接训练一个小的网络，没有小的网络根据大的网络来学习结果要来得好。

其实知识蒸馏也不是新的技术，知识蒸馏最知名的一篇文章 Hinton 在 15 年的时候已经发表论文了。很多人会觉得知识蒸馏是 Hinton 提出来的，因为 Hinton 有一篇论文“Distillingthe Knowledge in a Neural Network”。但其实在 Hinton 提出知识蒸馏这个概念之前，其实就有看过其他文章使用了一模一样的概念。举例来说，论文“Do Deep Nets Really Need to beDeep”是一篇 13 年的文章里面，也提出了网络蒸馏的想法。

为什么知识蒸馏会有帮助呢？一个比较直觉的解释是教师网络会提供学生网络额外的信息，如图 17.6 所示，如果直接跟学生网络这是 1，可能太难了。因为 1 可能跟其他的数字有点像，比如 1 跟 7 也有点像，1 跟 9 也长得有点像，所以对学生网络，我们告诉它：看到这张图片我们要输出 1。7 、9 的分数都要是 0，可能很难，它可能学不起来，所以让它直接去跟老师学，老师会告诉它这是 1。我们没有办法让它是 1 分，也没有关系。其实 1 跟 7 是有点像的，老师都分不出 1 跟 7 的差别。老师说 1 是 0.7，7 是 0.2，学生只要学到 1 是 0.7，7 是0.2 就够了。这样反而可以让小的网络，学得比直接从头开始训练，直接根据正确的答案要学来得要好。

Hinton 论文里面甚至可以做到教师告诉学生哪些数字之间有什么样的关系这件事情，就可以让学生在完全没有看到某些数字的训练数据下，就可以把那一个数字学会。假设训练数据里面完全没有数字 7 ，但是教师在学的时候有看过数字 7 ，但是学生从来没有看过数字 7。但光是凭着教师告诉学生说 1 跟 7 有点像，7 跟 9 有点像这样子的信息，都有机会让学生可以学到 7 长什么样子。就算它在训练的时候，从来没有看过 7 的训练数据。这是知识蒸馏的基本概念。

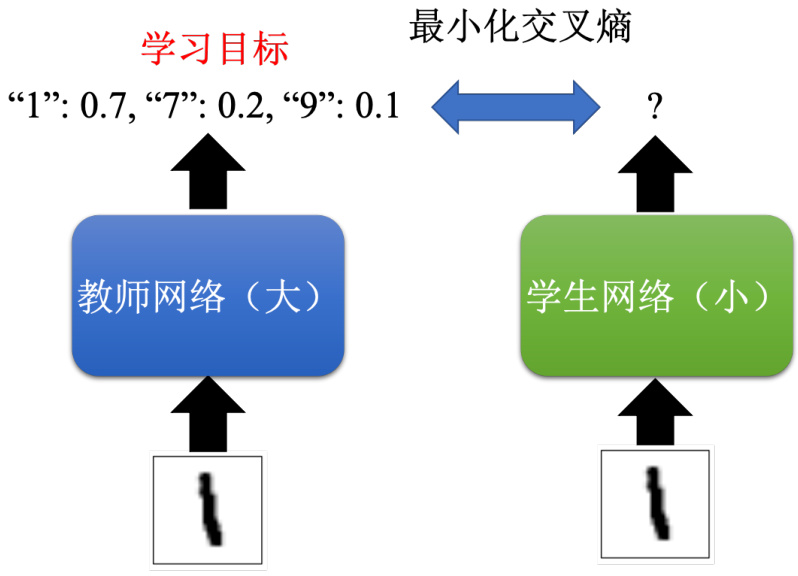
图 17.6 知识蒸馏

教师网络不一定要是单一的巨大网络，它甚至可以是多个网络的集成，训练多个模型，输出的结果就是多个模型，投票的结果就结束了。或者是把多个模型的输出平均起来的结果当做是最终的答案。虽然在比赛里面，常常会使用到集成的方法。如果在一个机器学习的比赛排行榜里面要名列前茅，往往凭借的就是集成技术，就是训练多个模型，把那么多的模型的结果通通平均起来。但是在实用上，集成会遇到的问题就训练了 1000 个模型，进来一笔数据，我们要 1000 个模型都跑过，再取它的平均，计算量也未免太大了。打比赛还勉强可以。要用在实际的系统上显然是不行的，可以把多个集成起来的网络综合起来变成一个，如图 17.7 所示。

这个就要用知识蒸馏的做法，就把多个网络集成起来的结果当做是教师网络的输出。让学生网络去学集成的结果，让学生网络去学集成的输出，让学生网络去逼进一堆网络集成起来的正确率。

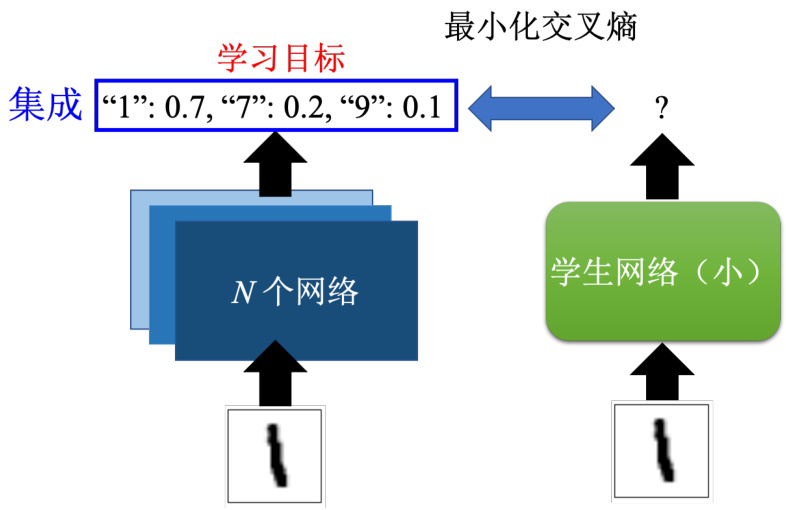
图 17.7 使用网络集成作为教师网络的输出

在使用知识蒸馏的时候有一个小技巧。这个小技巧是稍微改一下 Softmax 函数，会在Softmax 函数上面加一个温度（temperature）。Softmax 要做的事情就是把每一个神经元的输出都取指数，再做归一化，得到最终网络的输出，如式 (17.1) 所示。网络的输出变成一个概率的分布，网络最终的输出都是介于 0 到 1 之间的。所谓温度，就是在做取指数之前，把每一个数值都除上 $T$ ，如式 (17.2) 所示。

$$y_i^{\prime }=\frac{\exp \left(y_i\right)}{\sum _j\exp \left(y_j\right)}$$$$y_i^{\prime }=\frac{\exp \left(y_i/T\right)}{\sum _j\exp \left(y_j/T\right)}$$

其中 $T$ 是一个需要调整的超参数。假设 $T>1$ ，温度 $T$ 的作用就是把本来比较集中的分布变得比较平滑一点。举个例子，如式 (17.3) 所示，假设 $y_1,y_2,y_3$ 是原始的值， $y_1^{\prime },y_2^{\prime },y_3^{\prime }$ 是Softmax 后的值，softmax 后的值都趋近于 0。

$$\begin{array}{llll}{y}_1=100& y_1^{\prime }=1y_2=10& y_2^{\prime }\approx 0y_3=1& y_3^{\prime }\approx 0\end{array}$$

假设教师网络的输出如式 (17.3) 所示，让学生要叫教师网络去跟这个结果学，跟直接和正确的答案学完全没有不同。跟教师学的一个好处就是，老师会告诉我们说哪些类别其实是比较像的，让学生网络在学的时候不会那么辛苦。但是假设老师的输出非常地集中，其中某一个类别是 1，其他都是 0。这样子跟正确答案学没有不同，所以要取一个温度。假设温度 $T$ 设为 100，如式 (17.4)，对于教师，加上温度，分类的结果是不会变的。做完 Softmax 以后，最高分的还是最高分，最低分的还是最低分。所有类别的排序是不会变的，分类的结果是完全不会变的。但好处是每一个类别得到的分数会比较平滑、比较平均，我们拿这一个结果去给学生学才有意义，才能够把学生学得好。这是知识蒸馏的一个小技巧。

$$\begin{array}{llllll}{y}_1/T=1& y_1^{\prime }=0.56& y_2/T=0.1& y_2^{\prime }=0.23& y_3/T=0.01& y_3^{\prime }=0.21\end{array}$$

Q：拿 Softmax 前的输出来训练，会发生什么事呢？

A：完全可以拿 Softmax 前的输出来训练，其实还会有人拿网络的每一层都拿来训练。比如一个大的教师网络有 12 层，小的学生网络有 6 层。可以让学生网络第 6 层像大的网络的第 12 层，学生网络的第 3 层，像大的网络的第 6 层，可不可以呢。往往我们做这种比较多的限制，其实可以得到更好的结果。

温度太大，模型会会改变很多。假设温度接近无穷大，这样所有的类别的分数就变得差不多，学生网络也学不到东西了，因此 $T$ 又是另外一个超参数，它就跟学习率一样，这个是我们在做知识蒸馏的时候要调的参数。

17.3 参数量化

接下来介绍下一个技巧：参数量化（parameter quantization）。参数量化是说能否只用比较少的空间来储存一个参数。举个例子，现在存一个参数的时候可能是用 64 位或 32 位。可能不需要这么高的精度，用 16 或 8 位就够了。所以参数量化最简单的做法就是，本来如果存网络的时候，举例来说，我们是 16 个位存一个数值，现在改成 8 个位存一个数值。储存空间，网络的大小直接就变成原来的一半，而且性能不会掉很多，甚至有时候把储存参数的精度变低，结果还会稍微更好一点。还有一个再更进一步压缩参数的方法，即权重聚类（weightclustering）。

如图 17.8 所示，举个例子，先对网络的参数做聚类，按照这个参数的数值来分群。数值接近的放在一群，要分的群数会先事先设定好，比如设定好要分四群。比较相近的数字就被当做是一群。每一群都只拿一个数值来表示它。比如黄色的群所有数字的平均值是 0.4，就用$-0.4$ 来代表所有黄色的参数。储存参数时，就只要记两个东西：一个是表格，这个表格是记录说每一群代表的数值是多少。另外一个要记录的就是每一个参数属于哪一群。假设群的数量设少一点，比如说设四群，这样只要两个位就可以存一个参数了。本来存一个参数可能要16 位或 8 位，再进一步压缩到存一个参数只需要两个位就好。

其实还可以把参数再更进一步做压缩，使用哈夫曼编码（Huffman encoding）。哈夫曼编码的概念就是比较常出现的东西就用比较少的位来描述它，比较罕见的东西再用比较多的位来描述它。这样的好处平均起来，储存数据需要的位的数量就变少了，所以这个就是哈夫曼编码，所以可以用这些技巧来压缩参数，让我们储存每一个参数的时候需要的空间比较小，最终可以压缩到只拿一个位来存每一个参数。

网络里面的权重不是 $+1$ ，就是 −1。假设所有的权重只有正负 1 两种可能，每一个权重只需要一个位就可以存下来了。像这样子的这种二值权重（binary weight）的研究其实还蛮多的，具体可相关论文 。

虽然二值网络（binary network）参数值不是 $+1$ ，就是 −1，但这个网络的性能不一定会很差。二值网络里面的其中一个经典的方法，即二值连接（binary connect）。把二值连接这个技术用在三个图像识别的问题上，从最简单的 MNIST，还有稍微难一点的 CIFAR-10 以及

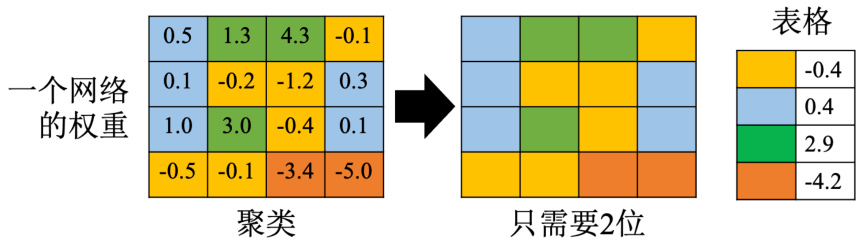
图 17.8 权重聚类

SVHN 数据集[4]。用二值连接结果居然是比较好的，所以用二值网络结果居然还比正常的网络的性能好一点。用二值网络的时候，给了网络比较大的限制，给网络容量（network capacity）比较大的限制，它比较不容易过拟合，所以用二值权重反而可以达到防止过拟合的效果。

Q：权重聚类要怎么做更新，每次更新都要重新分群吗？
A：其实权重聚类有一个很简单的做法。权重聚类是需要在训练的时候就考虑的。但是有一个简单的做法是，先把网络训练完，再直接做权重聚类。但这样直接做可能会导致聚类后的参数跟原来的参数相差太大。所以有一个做法是在训练的时候，要求网络的参数彼此之间比较接近。训练的量化可当做是损失的其中一个环节，直接塞到训练的过程中，让训练的过程中达到参数有权重聚类的效果。

Q：权重聚类里面每个聚类的数字要怎么决定呢?A：决定好每个聚类的区间之后, 取它们的平均。

17.4 网络架构设计

接下来介绍下网络架构的设计。通过网络架构的设计来达到减少参数量的效果。等一下要跟大家介绍深度可分离卷积（depthwise separable convolution）。在讲这个方法之前，先复习一下 CNN。在 CNN 的这种卷积层里面，每一个层的输入是一个特征映射。如图 17.9 所示，在这个例子里面，特征映射有两个通道，每一个滤波器的高度是 2，而且这个滤波器并不是一个长方形，而是一个立方体，通道有多少，的滤波器就得有多厚。再把这个滤波器扫过这个特征映射，就会得到另外一个正方形。我们有几个滤波器，输出特征映射就有几个通道。这边有 4 个滤波器，每一个滤波器都是立方体，输出特征映射就有 4 个通道。总共有 4 个滤波器，每一个滤波器的参数量是 $3\times 3\times 2$ ，要注意一下每一个滤波器，其实立方体总共的参数量是 $3\times 3\times 2\times 4=72$ 个参数。

接下来介绍下深度可分离卷积。深度可分离卷积分成两个步骤，第一个步骤称为深度卷积（depthwise convolution）。如图 17.10 所示，深度卷积要做的事情是有几个通道，我们就有几个滤波器，每一个滤波器只管一个通道。举例来说，假设输入特征映射是两个通道，在深度的卷积层里面，只放两个滤波器。不像之前在一般的卷积层里面，滤波器的数量跟通道的数量是无关的。图 17.9 中的通道只有两个，但滤波器可以有四个。但在深度卷积里面滤波器数量与通道数量相同，每一个滤波器就只负责一个通道而已。假设浅蓝色的滤波器管第一个通道，浅蓝色的滤波器在第一个通道上面滑过去，就算出一个特征映射。深蓝色的滤波器管第二个通道，它就在第二个通道上面做卷积，也得到另外一个特征映射。因此在深度卷积里面，输入有几个通道，输出的通道的数量会是一模一样的，这个跟一般的卷积层不一样。一般的卷积层里面，输入跟输出的通道数量可以不一样，但在深度卷积里面，输入跟输出的通道数量是一模一样的。

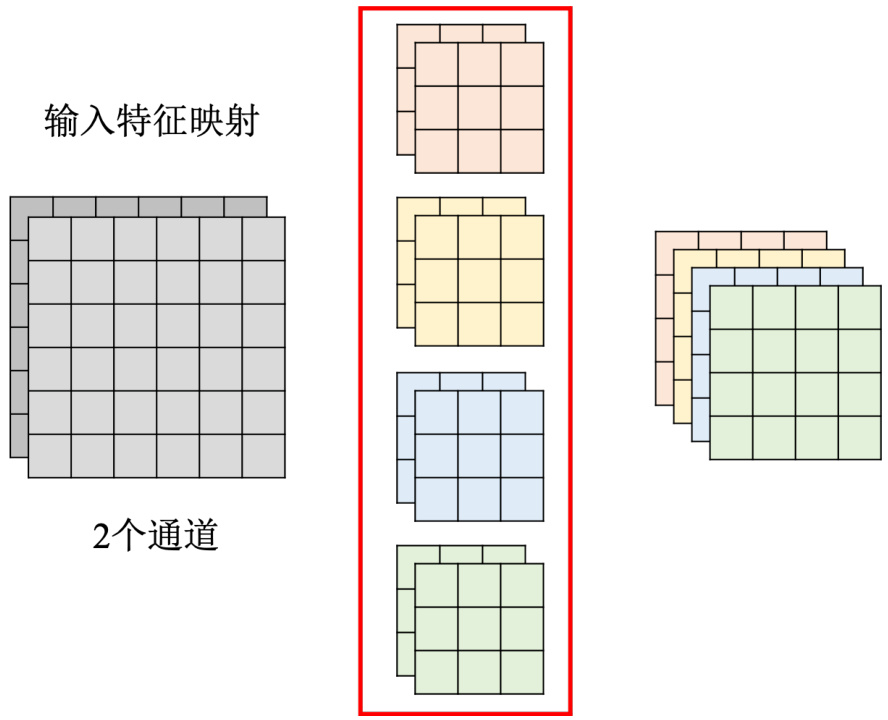
图 17.9 标准卷积

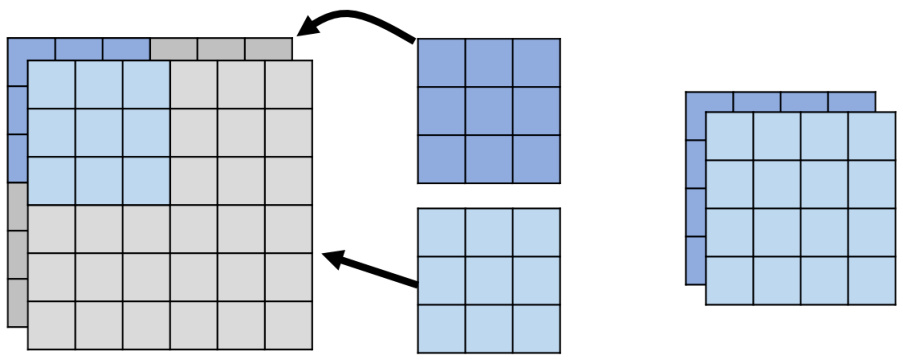
图 17.10 深度卷积

但是如果只做深度卷积，会遇到一个问题：通道和通道之间没有任何的互动。假设有某一个模式是跨通道才能够看得出来的，深度卷积对这种跨通道的模式是无能为力的，所以再多加一个点卷积。点卷积是指现在一样有一堆滤波器，这个跟一般的卷积层是一样的。但这边做一个限制是滤波器的大小，核大小通通都是 $1\times 1$ 。在一般的卷积层里面，滤波器大小可能开$2\times 2,3\times 3,4\times 4,$ 。但是在点卷积里面，我们限制大小一定是 $1\times 1$ 。如图 17.11 所示， $1\times 1$ 的滤波器的作用是去考虑不同通道之间的关系。所以第一个 $1\times 1$ 的滤波器就是去扫过这个深度卷积出来的特征映射，然后得到另外一个特征映射。这边有另外三个滤波器，它们做的事情也是一样，每一个滤波器会产生一个特征映射，所以点卷积跟一般的卷积层是一样的地方是，输入跟输出的通道数量可以不一样。但是点卷积有一个非常大的限制，强制要求滤波器的大小只准是 $1\times 1$ ，只要考虑通道之间的关系就好了，不要考虑同一个通道内部的关系了。深度卷积已经做完同一个通道内部的关系，所以点卷积只专注于考虑通道跟通道间的关系就好。

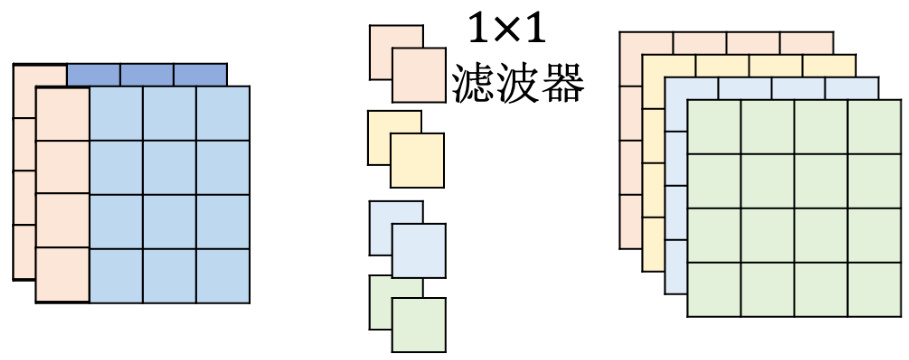
图 17.11 点卷积

如图 17.12 所示，先来计算一下这个方法的参数量。深度卷积里面两个滤波器，每一个滤波器大小是 $3\times 3$ ，所以总共是 $3\times 3\times 2=18$ 个参数。在点卷积里面，有四个滤波器，每一个滤波器的大小是 2，每个滤波器只用了两个参数，所以总共是 $2\times 4=8$ 个参数。左边图是一般的卷积，右边这个图是深度卷积加点卷积。

现在来比较一下这两者参数量的差异。假设我们先预设好，输入通道数量就是 $I$ 个通道，输出通道数量就是 $O$ 个通道。核大小都是 $k\times k$ 。如果是一般的卷积，要有 $k\times k$ 的核大小，输入 $I$ 个通道，输出 $O$ 个通道，到底会需要多少参数呢？每一个滤波器的大小应该是 $k\times k$ ，核大小乘上输入通道的数量也就是 $k\times k\times I$ 。如果要输出 $O$ 个通道，就需要 $O$ 个滤波器，一个滤波器的参数量是 $k\times k\times I$ 。总参数量是 $(k\times k\times I)\times O$

如果是深度卷积加点卷积，要达到输入 $I$ 个通道，输出 $O$ 个通道。深度卷积的滤波器是没有厚度的，它的滤波器是没有厚度的，所以深度卷积所有的滤波器加起来的参数量只有$k\times k\times I$ 而已，跟一般的卷积里面的一个滤波器的参数量是一样的。点卷积的参数量是 $I\times O$ 。假设输入通道的数量是 $I$ ，每一个 $1\times 1$ 的卷积的高度会是 $I$ 。假设要输出 $O$ 个通道，就要有 $O$ 个 $1\times 1$ 的卷积，所以点卷积的总参数量是 $I\times O$ 。如式 (17.5) 所示，把这两者进行比较，因为 $O$ 通常是一个很大的值，通道数量可能设置为 256 或 512 ，所以先忽略 $\frac{1}{O}$ ， $\frac{1}{k\times k}$ 通常是比较在这一整项里面是比较关键的数值。这一整项的大小跟 $\frac{1}{k\times k}$ 是比较有关系的。假设核大小可能是 $3\times 3$ 或者是 $2\times 2$ 。假设核大小是 $2\times 2$ ，把一般的卷积换成深度卷积加点卷积组合的话，网络大小就变成 $\frac{1}{4}$ 。假设核大小是 $3\times 3$ ，从卷积变成深度卷积加点卷积的时候，网络大小就变成原来的 $\frac{1}{9}$ 。

$$\begin{array}{l}{\displaystyle \frac{k\times k\times I+I\times O}{k\times k\times I\times O}}{\displaystyle =\frac{1}{O}+\frac{1}{k\times k}}\end{array}$$

在深度可分离卷积之前，就已经有一个方法是用低秩近似（low rank approximation）来减少一层网络的参数量。如图 17.13 所示，假设有某一个层有 $N$ 个神经元，输出有 $M$ 个神经元。假设输入是 $N$ 个神经元，输出是 $M$ 个神经元，这两层之间的参数量是 $N\times M$ 。只要$N$ 跟 $M$ 其中一者很大， $W$ 的参数就很多了。怎么减少这个参数量呢？有一个非常简单的方法是在 $N$ 跟 $M$ 中间再插一层，这一层就不用激活函数，这一层神经元的数量是 $K$ 。原来本来只有一层，现在拆成两层，这两层里面的第一层用 $V$ 来表示，第二层用 $U$ 来表示。这两层的网络参数量反而是比较少的。原来一层的网络的参数量是 $M\times N$ 。如果拆成两层网络，第一层是 $N\times K$ ，第二层是 $K\times M$ 。如果 $K$ 远小于 $M$ 跟 $N$ ， $U$ 跟 $V$ 的参数量加起来是比

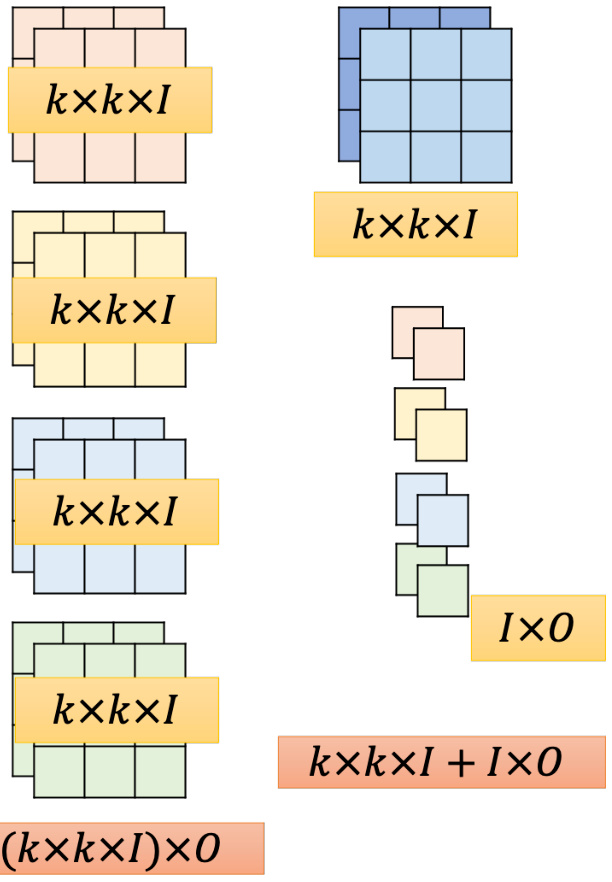
图 17.12 深度可分离卷积参数计算

$W$ 还要少的多。 $W$ 是 $N\times M$ ， $U$ 跟 $V$ 的参数量加起来是 $K\times (N+M)$ ，只要 $K$ 够小，整体而言 $U+V$ 的参数量就会变少。之前过去常有的做法就是 $N=1000,M=1000$ ，可以塞个 20 或 50，参数量就减少蛮多的。这样子的方法虽然可以减少参数量，但它还是会有一些限制。把 $W$ 拆解成 $U\times V$ 的时候，把 $W$ 用 $U$ 跟 $V$ 两层来分开表示的时候，我们会减少 $W$ 的可能性，本来 $W$ 可以放任何的参数。但假设把 $W$ 拆成 $U$ 跟 $V$ ，矩阵 $W$ 的秩会小于等于$K$ 。如果不知道秩是什么也没有关系，反正就是 $W$ 会有一些限制，所以会变成说不是所有的$W$ 都可以变成当作参数，参数会变成有一些限制。这个方法就是拿来减少参数的一个非常常用的做法。其实刚才讲的深度卷积加点卷积（pointwise convolution）其实用的就是把一层拆成两层的概念。

怎么说呢？如图 17.14 所示，先来看一下原来的卷积。在原来的卷积里面，左上角红色的这一个矩的这个参数是怎么来的。是不是有一个红色的这个滤波器放在特征输入的特征映射的左上角以后所得到的。在这个例子里面，一个滤波器的参数量是 $3\times 3\times 2=18$ ，把滤波器里面的 18 个参数跟输入特征映射左上角的这 18 个数值做内积以后，就会得到这边输出特征映射左上角的值，所以每一个滤波器有 18 个参数。

如果拆成深度卷积加点卷积两阶段，左上角输出特征映射，左上角这个数值来自于中间的深度卷积的输出。所以左上角这个值来自于中间深度卷积的输出，左上角这两个值来自于输入特征映射，第一个通道左上角这 9 个值跟第二个通道左上角这 9 个值。我们有两个滤波器，这两个滤波器分别是 9 个输入，得到输出，接下来这两个滤波器的输出再把它综合起来，得到最终的输出。所以本来是直接从这 18 个数值变成一个数值，现在是分两阶，18 个数值变两个数值再变一个数值。如果看黄色的这个特征映射左下角这个参数黄色的特征映射。左下角来自于深度卷积的输出。而左下角这两个数值来自于这个滤波器左下这来自于这个深度卷积，来自于输入的这个特征映射。左下角的这 18 个数值，把一般的卷积拆成深度卷积加点卷积的时候，就可以看成是把一层的网络拆解成两层的网络，其原理跟低秩近似是一样的，把一层拆成两层，这个时候它对于参数的需求反而是减少了，这个是有关网络架构（networkarchitecture）的设计。

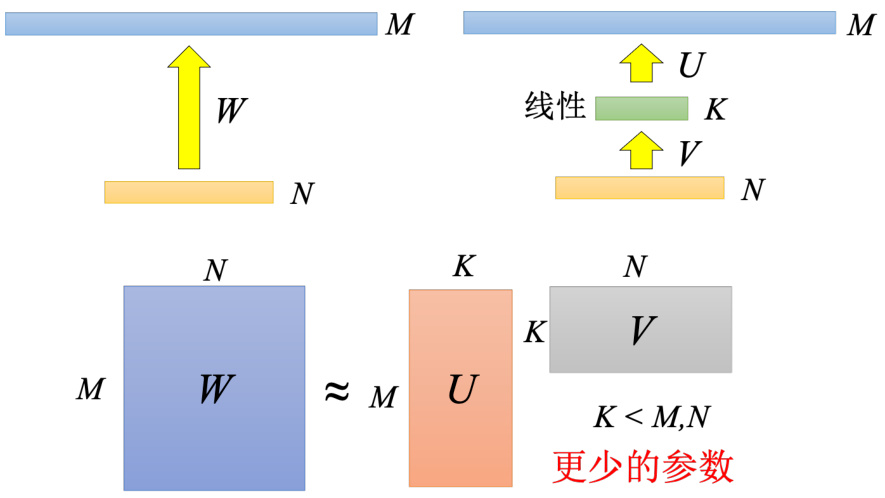
图 17.13 低秩近似示例

图 17.14 标准卷积与深度可分离卷积对比

17.5 动态计算

最后一个介绍的方法是动态计算（dynamic computation）。动态计算跟前几个方法想要达成的目标不太一样。前几个方法就是单纯的把网络变小，而动态计算希望网络可以自由地调整它需要的计算量。为什么期待网络可以自由地调整它需要的计算量呢? 因为有时候我们可能同样的模型会想要跑在不同的设备上面，而不同的设备上面的计算资源是不太一样的。

所以期待训练好一个网络以后，放到新的设备上面，不需要再重训练这个网络。因为这个训练一个神奇的模型，这个神奇的模型本来就可以自由调整所需要的计算资源。计算资源少的时候只需要少的计算资源，就可以计算。计算资源大的时候，它就可以充分利用充足的计算资源来进行计算。那另外一个可能是就算是在同一个设备上面，也会需要不同的计算。举个例子，假设手机非常有电，可能就会有比较多的计算资源。假设手机没电，可能就需要把计算资源留着做其他的事情，网络可能可以分到的计算资源就比较少，所以就算是在同一个设备上面。我们也希望一个网络可以根据现有的计算资源，比如说手机现在的电量还有多少来自由地调整它对计算量的需求。

Q：为什么不直接准备一大堆的网络，假设需要各种应付各种不同计算资源的情况，为什么不训练 10 个网络，从计算量最少的到计算量最大的，根据计算的情况去选择不同的网络呢？

A：假设我们是在同一台手机上，需要根据不同的情况做不同的因应，可能就需要训练大堆的网络。而手机上的储存空间有限，就是要减少计算量。但是如果我们需要训练一大堆的网络，就需要一大堆的储存空间。这可能不是我们要的，其实期待可以做到一个网络可以自由地调整其对计算资源的需求。

怎么让网络自由地调整其对计算资源的需求呢？一个可能的方向是让网络自由地调整它的深度。比如图像分类，如图 17.15 所示，它就是输入一张图片，输出是图片分类的结果，可以在这个层和层中间再加上一个额外的层。这个额外的层的工作是根据每一个隐藏层的输出决定现在分类的结果。当计算资源比较充足的时候，可以让这张图片去跑过所有的层，得到最终的分类结果。当计算资源不充足的时候，可以让网络决定它要在哪一个层自行做输出。比如说计算资源比较不充足的时候，通过第一个层，就直接丢到这个额外的第 1 层，就得到最终的结果了。怎么训练这样一个网络呢？其实概念比我们想像的还要简单，训练的时候都有标签的数据。一般在训练的时候，只需要在意最后一层网络的输出，希望它的输出跟标准答案越接近越好。但也可以让标准答案跟每一个额外层的输出越接近越好。把所有的输出跟标准答案的距离通通加起来，把所有的输出跟标准答案的交叉熵通通加起来得到 $L$

$$\mathcal{L}=e_1+e_2+\cdot \cdot \cdot +e_L$$

再去最小化这个 $L$ ，然后就结束了，这个训练方法是可以用的。确实可以用我刚才讲的训练方法，就是每一层接出来做训练，然后把所有接出来的结果去跟标准答案算距离，最小化所有接出来的结果跟标准答案的距离，确实可以用这个方法达到动态的深度，但是其实它不是一个最好的方法。

比较好的方法可以参考 MSDNet[7]。另外还可以让网络自由地决定它的宽度，怎么让网络自由决定它的宽度。设定好几个不同的宽度，同一张图片丢进去。在训练的时候，同一张图片丢进去，每个不同宽度的网络会有不同的输出。我们在希望每一个输出都跟正确答案越接近越好就结束了，把所有的输出跟标准答案的距离加起来得到一个损失，最小化这个损失就结束了。

$$\mathcal{L}=e_1+e_2+e_3$$

图 17.16 中的三个网络并不是三个不同的网络，它们是同一个网络可以选择不同的宽度。

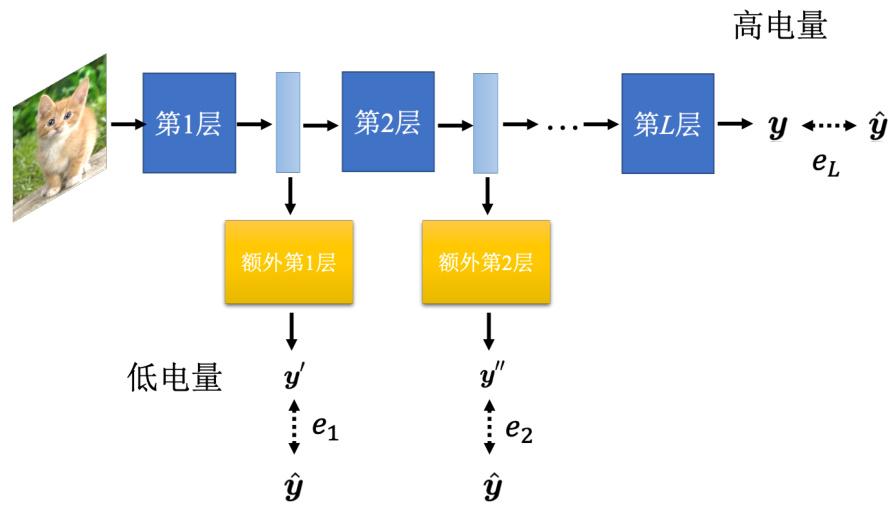
图 17.15 动态深度

相同颜色是同一个权重。只是在最左边情况的时候，整个网络所有的神经元都会被用到。但是在中间情况的时候，可能会决定有 $25\mathrm{\%}$ 的神经元不需要用。或者在最右边的情况， $50\mathrm{\%}$ 的神经元不要用它。在训练的时候，就把所有的情况一起考虑，然后所有的情况都得到一个输出，所有的输出都去跟标准答案计算距离，要让所有的距离都越小越好就结束了。但是实际上这样训练也是有问题的。所以需要一些特别的想法来解决这个问题。

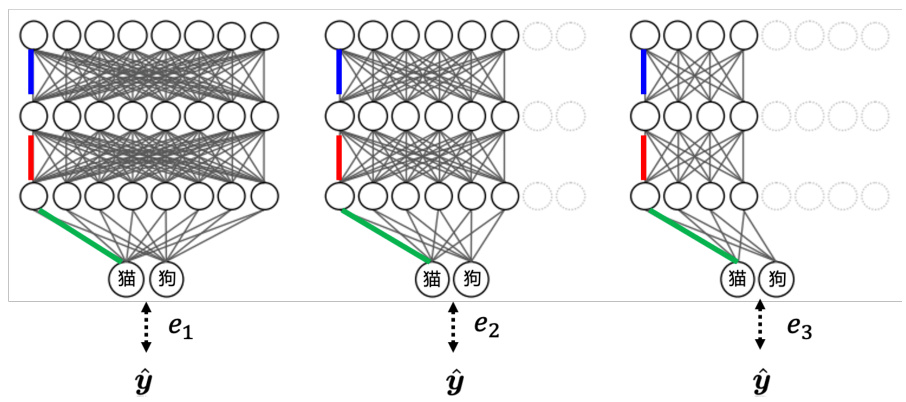
图 17.16 动态宽度

有关深度（depthwise）动态的宽度的网络，怎么训练这件事？大家可以参考论文“SlimmableNeural Networks”[8]。那刚才讲的是可以训练一个网络，可以自由去决定它的深度跟宽度。但是还需要我们去决定，今天电池电量少于多少的时候，就用多少层或者是多宽的网络。但是有没有办法让网络自行决定，根据情况决定它的宽度或者是深度呢。

Q：为什么需要网络自己去决定它的宽度跟深度呢？A：因为有时候，就算是同样是图像分类的问题，图像的难易程度不同，有些图像可能特别难，有些图像可能特别简单。对那些比较简单的图像，也许只要通过一层网络就已经可以知道答案了，对于一些比较难的问题，需要多层网络才能知道答案。

举例来说，如图 17.17 所示，同样是猫，但有只猫是被做成一个墨西哥卷饼，所以这是一个特别困难的问题。也许这张图片只通过一个层的时候，网络会觉得它是一个卷饼；在通过第二个层的时候，还是一个卷饼。要通过很多个层的时候，网络才能够判断它是一只猫。这种比较难的问题就不应该在中间停下来。可以让网络自己决定这是一张简单的图片，所以通过第一层就停下来。这是一个比较困难的图片，要跑到最后一层才停下来。具体怎么做可参考论文“SkipNet: Learning Dynamic Routing in Convolutional Networks”[9]、Runtime NeuralPruning[10] 和“BlockDrop: Dynamic Inference Paths in Residual Networks”[11]。

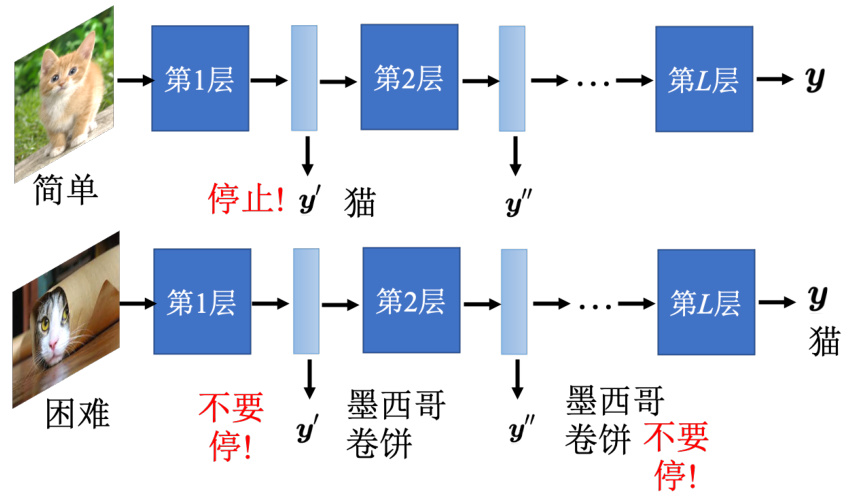
图 17.17 计算量取决于采样难度

所以像这种方法不一定限制在计算资源比较有限的情况。有时候就算计算资源比较很充足，但是对一些简单的图片，如果可以用比较少的层，得到需要的结果，其实也就够了，这样就可以省下一些计算资源去做其他的事情。

以上就是网络压缩的五个技术。前面四个技术都是让网络可以变小，这四个技术并不是互斥的。其实在做网络压缩的时候，可以既用网络架构，也做知识蒸馏，还可以在做完知识蒸馏以后，再去做网络剪枝。还可以在做完网络剪枝以后，再去做参数量化。如果想要把网络压缩到很小，这些方法都是可以一起被使用的。

参考文献

[1] WEN W, WU C, WANG Y, et al. Learning structured sparsity in deep neural networks [J]. Advances in neural information processing systems, 2016, 29.
[2] ZHOU H, LAN J, LIU R, et al. Deconstructing lottery tickets: Zeros, signs, and the supermask[J]. Advances in neural information processing systems, 2019, 32.
[3] LIU Z, SUN M, ZHOU T, et al. Rethinking the value of network pruning[C]//ICLR. 2019.
[4] COURBARIAUX M, BENGIO Y, DAVID J P. Binaryconnect: Training deep neural networks with binary weights during propagations[J]. Advances in neural information processing systems, 2015, 28.
[5] COURBARIAUX M, HUBARA I, SOUDRY D, et al. Binarized neural networks: Training deep neural networks with weights and activations constrained to ${}^{+}$ 1 or-1[J]. arXiv preprint arXiv:1602.02830, 2016.
[6] RASTEGARI M, ORDONEZ V, REDMON J, et al. Xnor-net: Imagenet classification using binary convolutional neural networks[C]//European conference on computer vision. Springer, 2016: 525-542.
[7] HUANG G, CHEN D, LI T, et al. Multi-scale dense networks for resource efficient image classification[C]//ICLR. 2018.
[8] YU J, YANG L, XU N, et al. Slimmable neural networks[C]//ICLR. 2019.
[9] WANG X, YU F, DOU Z Y, et al. Skipnet: Learning dynamic routing in convolutional networks[C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 409-424.
[10] LIN J, RAO Y, LU J, et al. Runtime neural pruning[J]. Advances in neural information processing systems, 2017, 30.
[11] WU Z, NAGARAJAN T, KUMAR A, et al. Blockdrop: Dynamic inference paths in residual networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 8817-8826.