Classification: Probabilistic Generative Model
Classification
概念描述
分类问题是找一个function,它的input是一个object,它的输出是这个object属于哪一个class
还是以宝可梦为例,已知宝可梦有18种属性,现在要解决的分类问题就是做一个宝可梦种类的分类器,我们要找一个function,这个function的input是某一只宝可梦,它的output就是这只宝可梦属于这18类别中的哪一个type

输入数值化
对于宝可梦的分类问题来说,我们需要解决的第一个问题就是,怎么把某一只宝可梦当做function的input?
==要想把一个东西当做function的input,就需要把它数值化==
特性数值化:用一组数字来描述一只宝可梦的特性
比如用一组数字表示它有多强(total strong)、它的生命值(HP)、它的攻击力(Attack)、它的防御力(Defense)、它的特殊攻击力(Special Attack)、它的特殊攻击的防御力(Special defend)、它的速度(Speed)
以皮卡丘为例,我们可以用以上七种特性的数值所组成的vector来描述它

How to classification
Training data for Classification
假设我们把编号400以下的宝可梦当做training data,编号400以上的当做testing data,因为宝可梦随着版本更新是不断增加的,编号比较前面的宝可梦是比较早发现的,所以我们去模拟已经发现这些宝可梦的情况下,如果看到新的宝可梦,能不能够预测它是哪种属性
Classification as Regression?
可以把分类问题当做回归问题来解吗?
以binary classification为例,我们在Training时让输入为class 1的输出为1,输入为class 2的输出为-1;那么在testing的时候,regression的output是一个数值,它接近1则说明它是class 1,它接近-1则说明它是class 2
如果这样做,会遇到什么样的问题?
假设现在我们的model是
有两个class,蓝色的是class 1,红色的是class 2,如果用Regression的做法,那么就希望蓝色的这些属于class 1的宝可梦,input到Regression的model,output越接近1越好;红色的属于class 2的宝可梦,input到Regression的model,output越接近-1越好
假设我们真的找到了这个function,就像下图左边所示,绿色的线表示
但是上述现象只会出现在样本点比较集中地分布在output为-1和1的情况,如果像下图右侧所示,我们已经知道绿线为最好的那个model的分界线,它的左上角的值小于0,右下角的值大于0,越往右下方值越大,所以如果要考虑右下角这些点的话,用绿线对应的model,它们做Regression的时候output会是远大于1的,但是你做Regression的时候,实际上已经给所有的点打上了-1或1的标签(把-1或1当做“真值”),你会希望这些紫色点在model中的output都越接近1(接近所谓的“真值”)越好,所以这些output远大于1的点,它对于绿线对应的model来说是error,是不好的,所以这组样本点通过Regression训练出来的model,会是紫色这条分界线对应的model,因为相对于绿线,它“减小”了由右下角这些点所带来的error
Regression的output是连续性质的数值,而classification要求的output是离散性质的点,我们很难找到一个Regression的function使大部分样本点的output都集中在某几个离散的点附近
因此,Regression定义model好坏的定义方式对classification来说是不适用的
注:该图为三维图像在二维图像上的投影,颜色表示y的大小
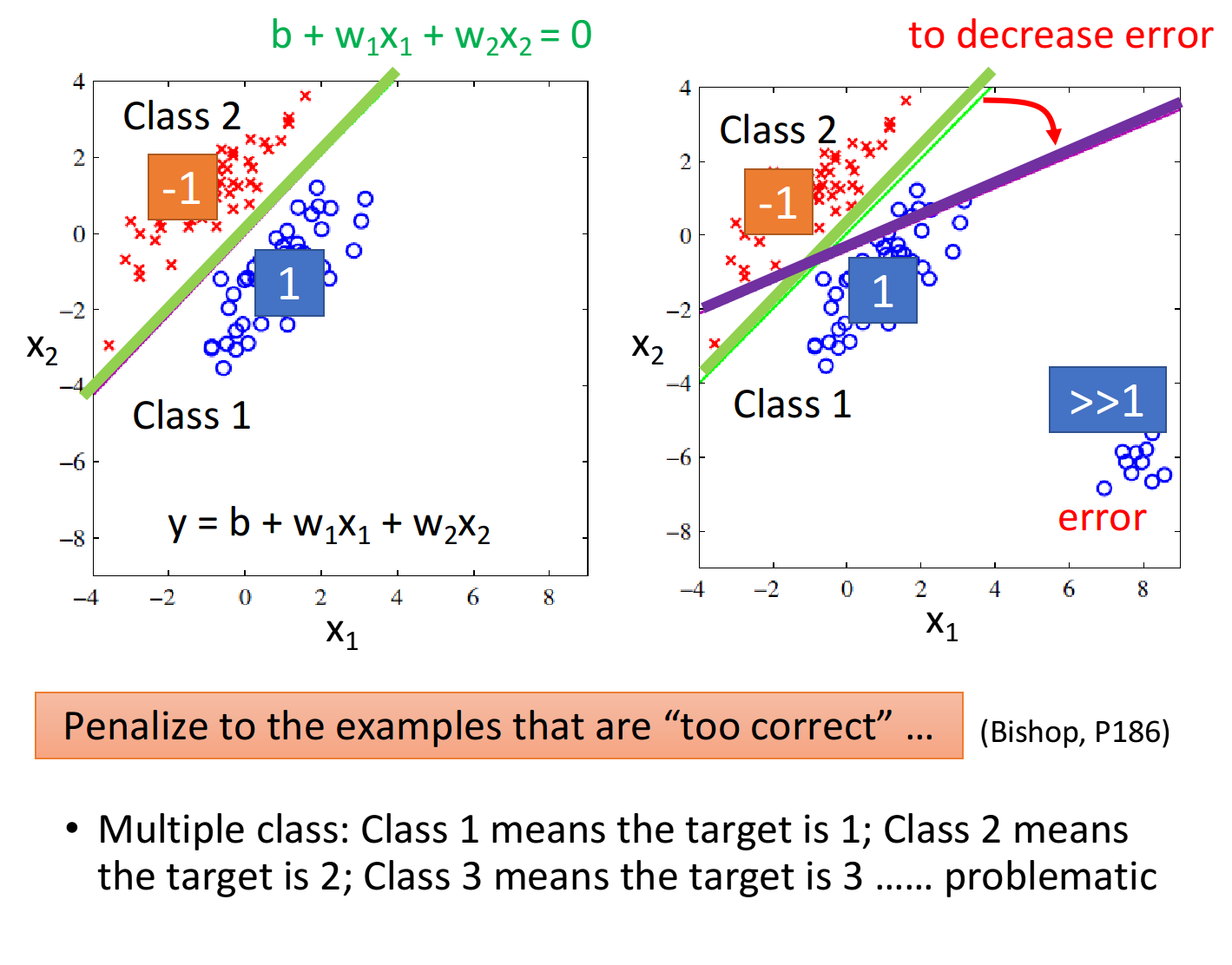
而且值得注意的是,如果是多元分类问题,把class 1的target当做是1,class 2的target当做是2,class 3的target当做是3的做法是错误的,因为当你这样做的时候,就会被Regression认为class 1和class 2的关系是比较接近的,class 2和class 3的关系是比较接近的,而class 1和class 3的关系是比较疏远的;但是当这些class之间并没有什么特殊的关系的时候,这样的标签用Regression是没有办法得到好的结果的(one-hot编码也许是一种解决方案?)
Ideal Alternatives
注意到Regression的output是一个real number,但是在classification的时候,它的output是discrete(用来表示某一个class)
理想的方法是这样的:
Function(Model)
我们要找的function f(x)里面会有另外一个function g(x),当我们的input x输入后,如果g(x)>0,那f(x)的输出就是class 1,如果g(x)<0,那f(x)的输出就是class 2,这个方法保证了function的output都是离散的表示class的数值

那之前不是说输出是1,2,3...是不行的吗,注意,那是针对Regression的loss function而言的,因为Regression的loss function是用output与“真值”的平方和作为评判标准的,这样输出值(3,2)与(3,1)之间显然是(3,2)关系更密切一些,为了解决这个问题,我们只需要重新定义一个loss function即可
Loss function
我们可以把loss function定义成
但是这个loss function没有办法微分,是无法用gradient descent的方法去解的,当然有Perceptron、SVM这些方法可以用,但这里先用另外一个solution来解决这个问题
Solution:Generative model
概率理论解释
假设我们考虑一个二元分类的问题,我们拿到一个input x,想要知道这个x属于class 1或class 2的概率
实际上就是一个贝叶斯公式,x属于class 1的概率就等于class 1自身发生的概率乘上在class 1里取出x这种颜色的球的概率除以在class 1和 class 2里取出x这种颜色的球的概率(后者是全概率公式)
==贝叶斯公式=单条路径概率/所有路径概率和==
graph LR
A(摸球) -->|从class 1里摸球的概率| B(class 1)
A -->|从class 2里摸球的概率| C(class 2)
B -->|在class 1里摸到x的概率|D(摸到x)
C -->|在class 2里摸到x的概率|D因此我们想要知道x属于class 1或是class 2的概率,只需要知道4个值:
流程图简化如下:
graph LR
A(begin)
A--> |"P(C1)"| B(Class 1)
A--> |"P(C2)"| C(Class 2)
B--> |"P(x|C1)"| D(x)
C--> |"P(x|C2)"| D(x)于是我们得到:(分母为全概率公式)
- x属于Class 1的概率为第一条路径除以两条路径和:
- x属于Class 2的概率为第二条路径除以两条路径和:
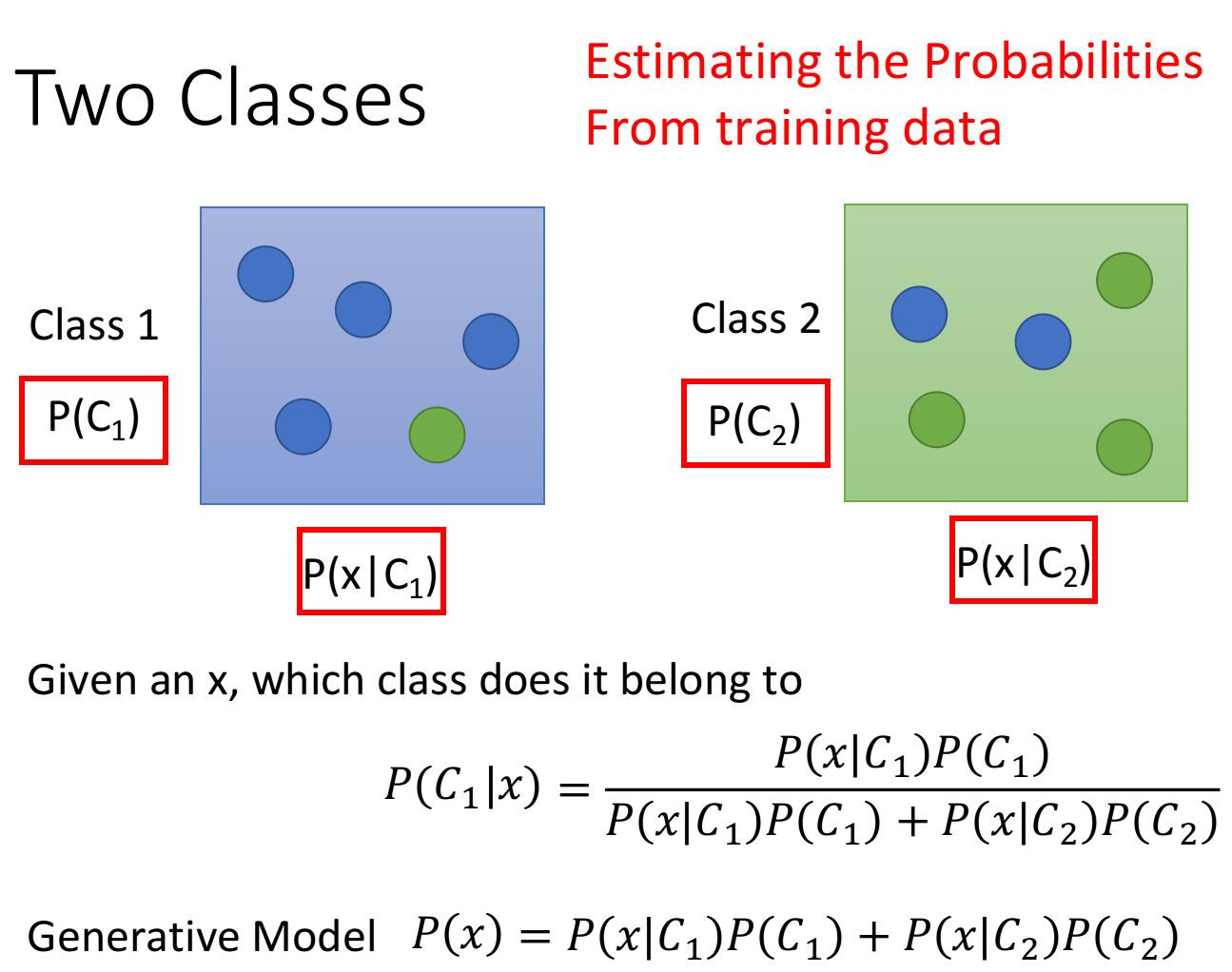
这一整套想法叫做Generative model(生成模型),为什么叫它Generative model呢?因为有这个model的话,就可以拿它来generate生成x(如果你可以计算出每一个x出现的概率,就可以用这个distribution分布来生成x、sample x出来)
Prior
假设我们还是考虑二元分类问题,编号小于400的data用来Training,编号大于400的data用来testing,如果想要严谨一点,可以在Training data里面分一部分validation出来模拟testing的情况
在Training data里面,有79只水系宝可梦,61只一般系宝可梦,那么
现在的问题是,怎么得到
Probability from Class
怎么得到
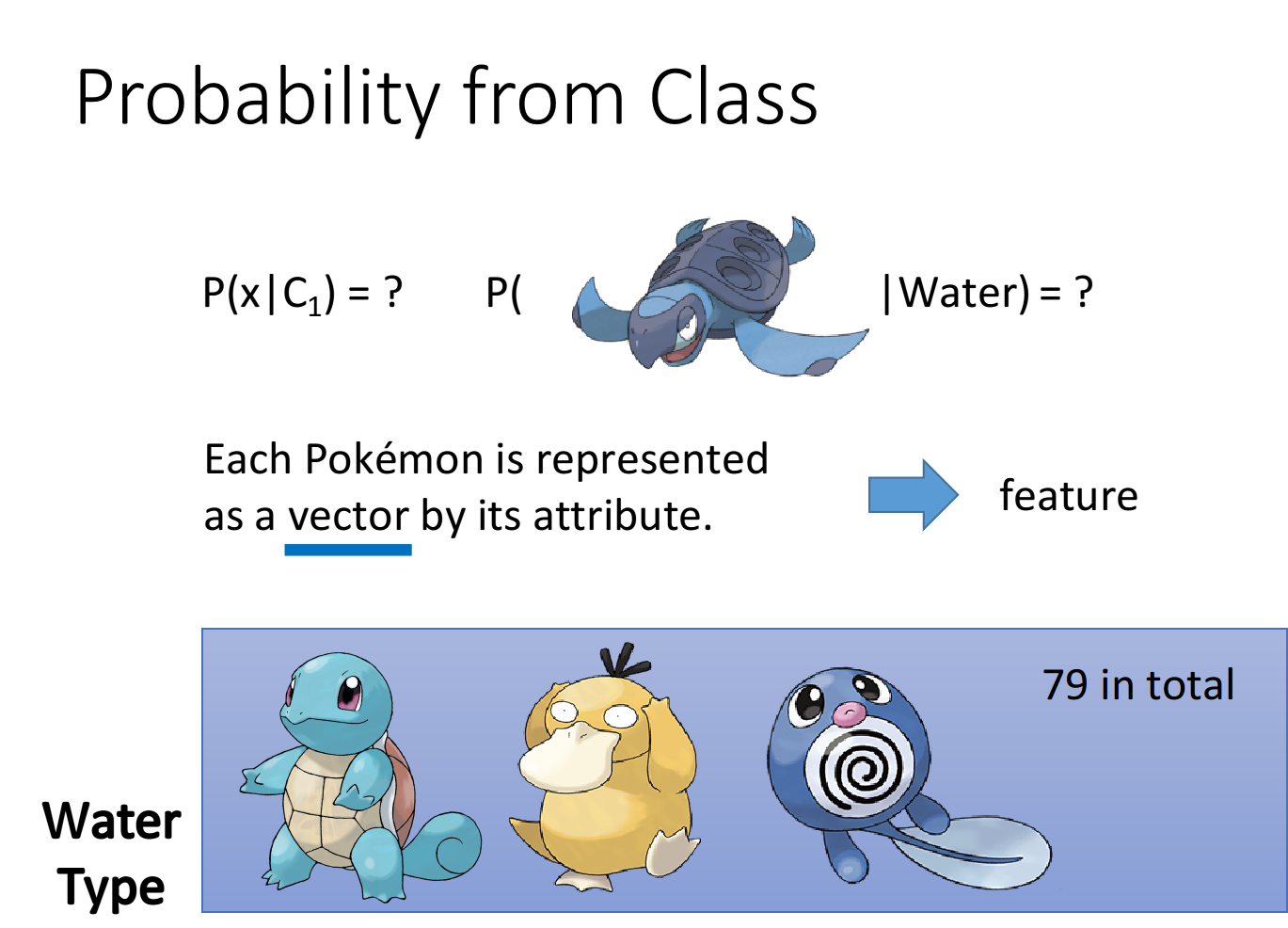
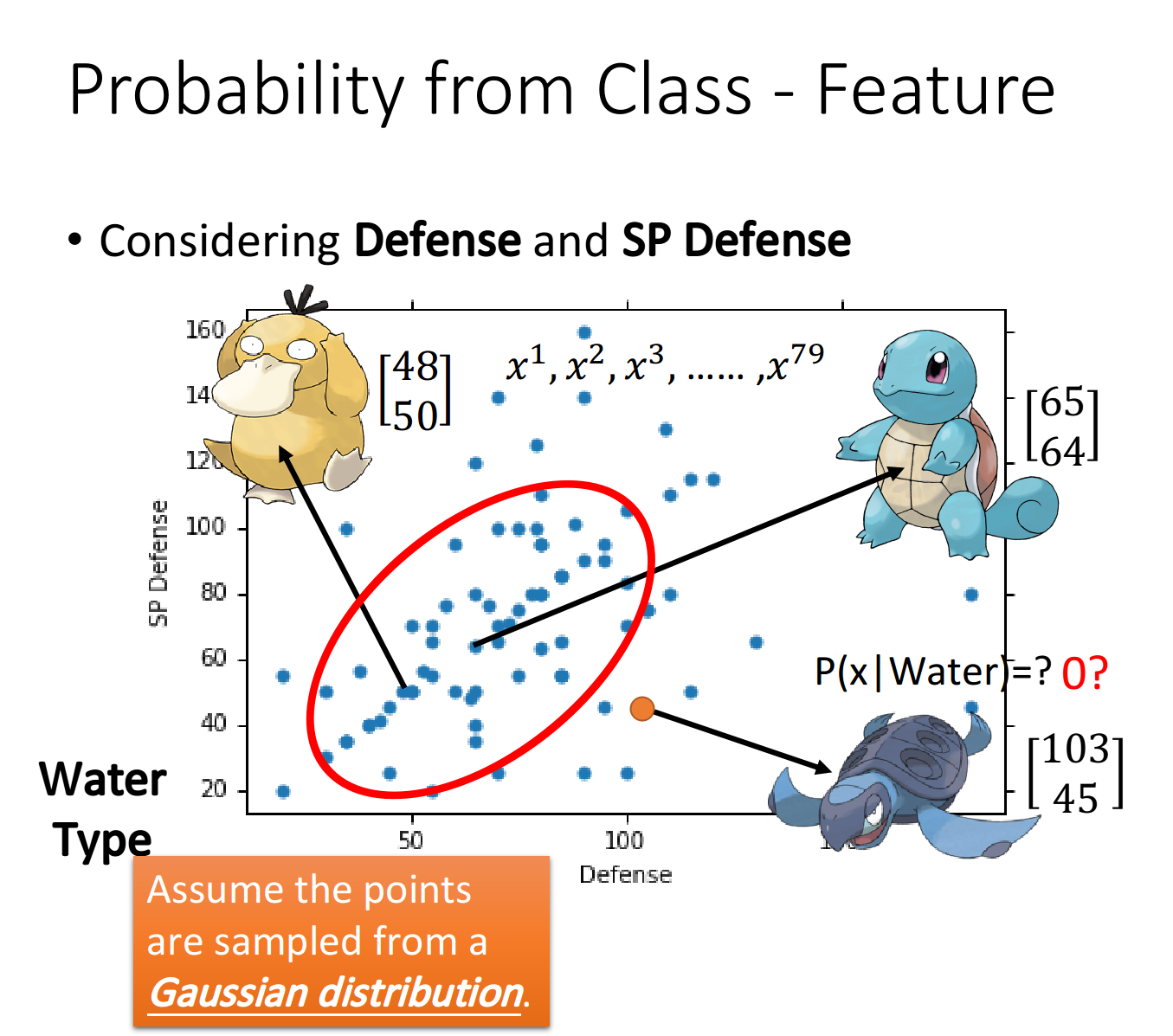
其实每一只宝可梦都是用一组特征值组成的向量来表示的,在这个vector里一共有七种不同的feature,为了方便可视化,这里先只考虑Defense和SP Defence这两种feature
假设海龟的vector是[103 45],虽然这个点在已有的数据里并没有出现过,但是不可以认为它出现的概率为0,我们需要用已有的数据去估测海龟出现的可能性
你可以想象说这已有的79只水系宝可梦的data其实只是冰山一角,假定水系神奇宝贝的Defense和SP Defense是从一个Gaussian的distribution里面sample出来的,下图只是采样了79个点之后得到的分布,但是从高斯分布里采样出海龟这个点的几率并不是0,那从这79个已有的点,怎么找到那个Gaussian distribution函数呢?
Gaussian Distribution
先介绍一下高斯函数,这里
从下图中可以看出,同样的
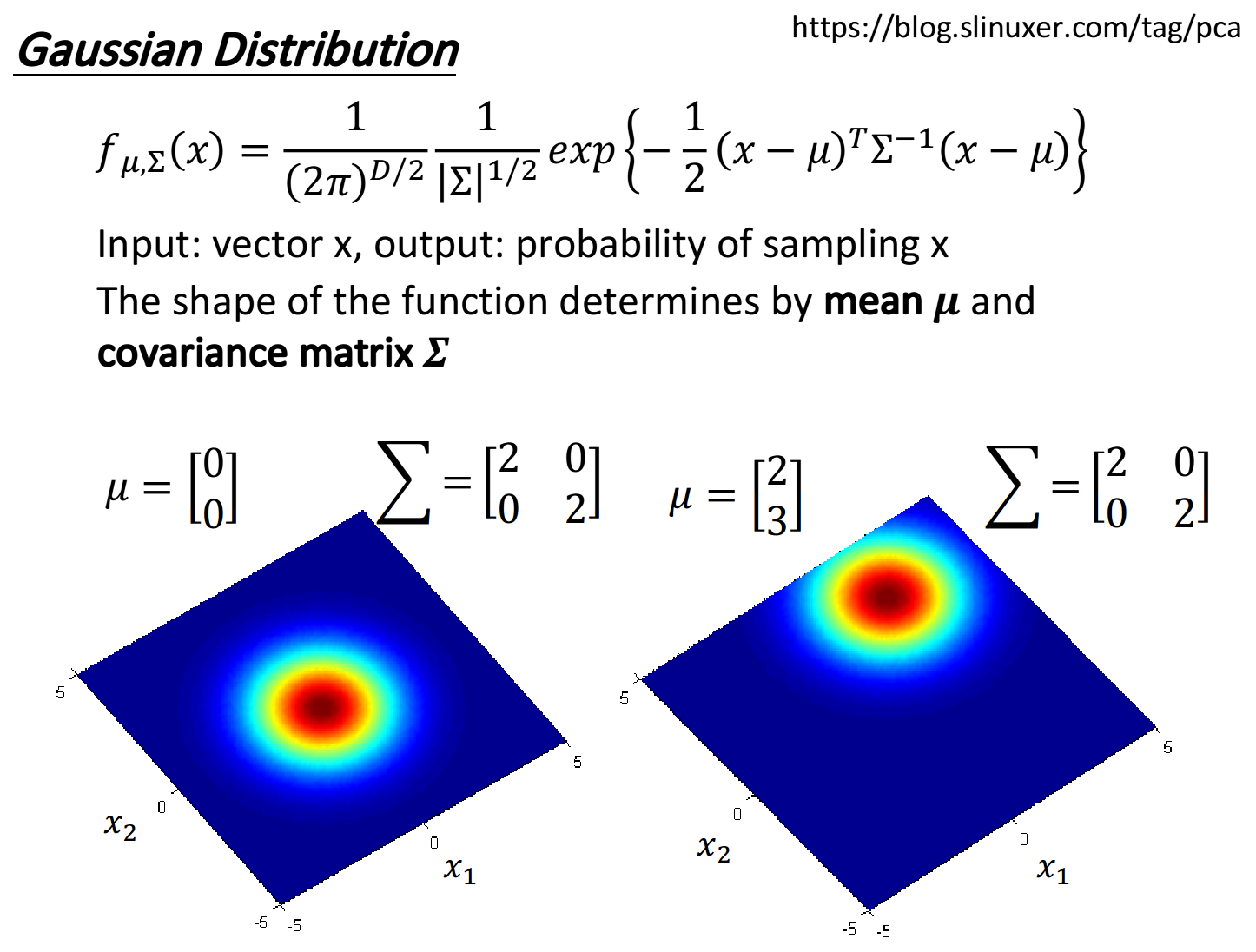
同理,如果是同样的
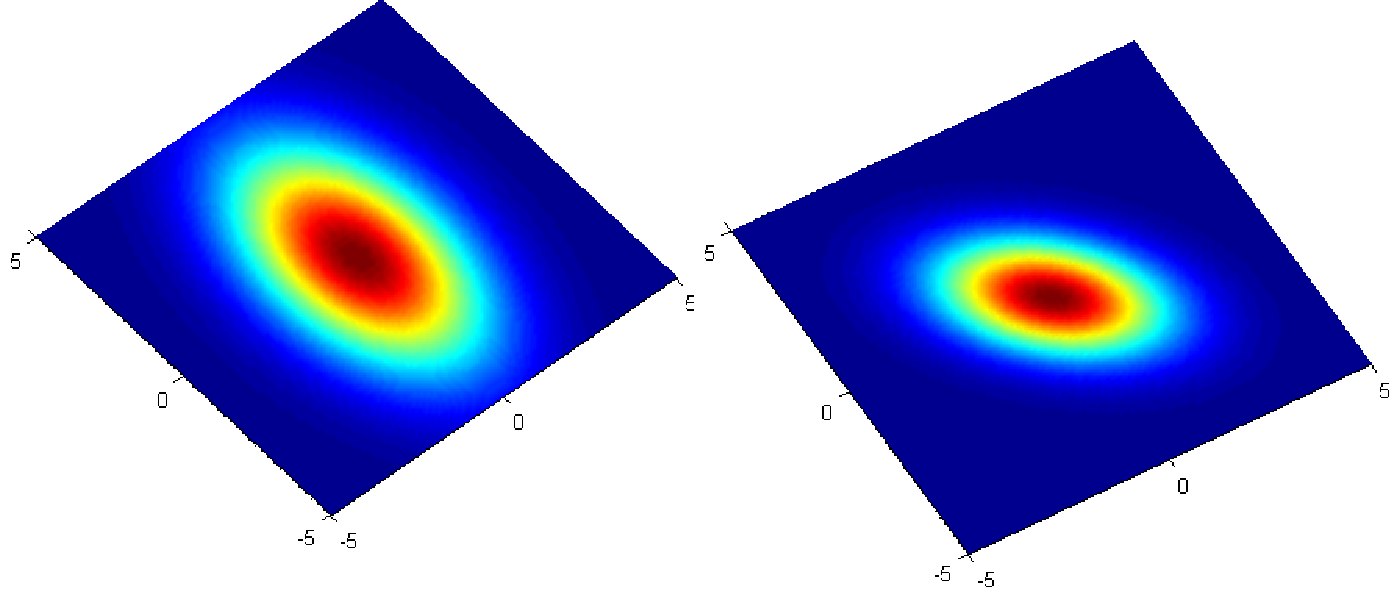
那接下来的问题就是怎么去找出这个Gaussian,只需要去估测出这个Gaussian的均值
估测
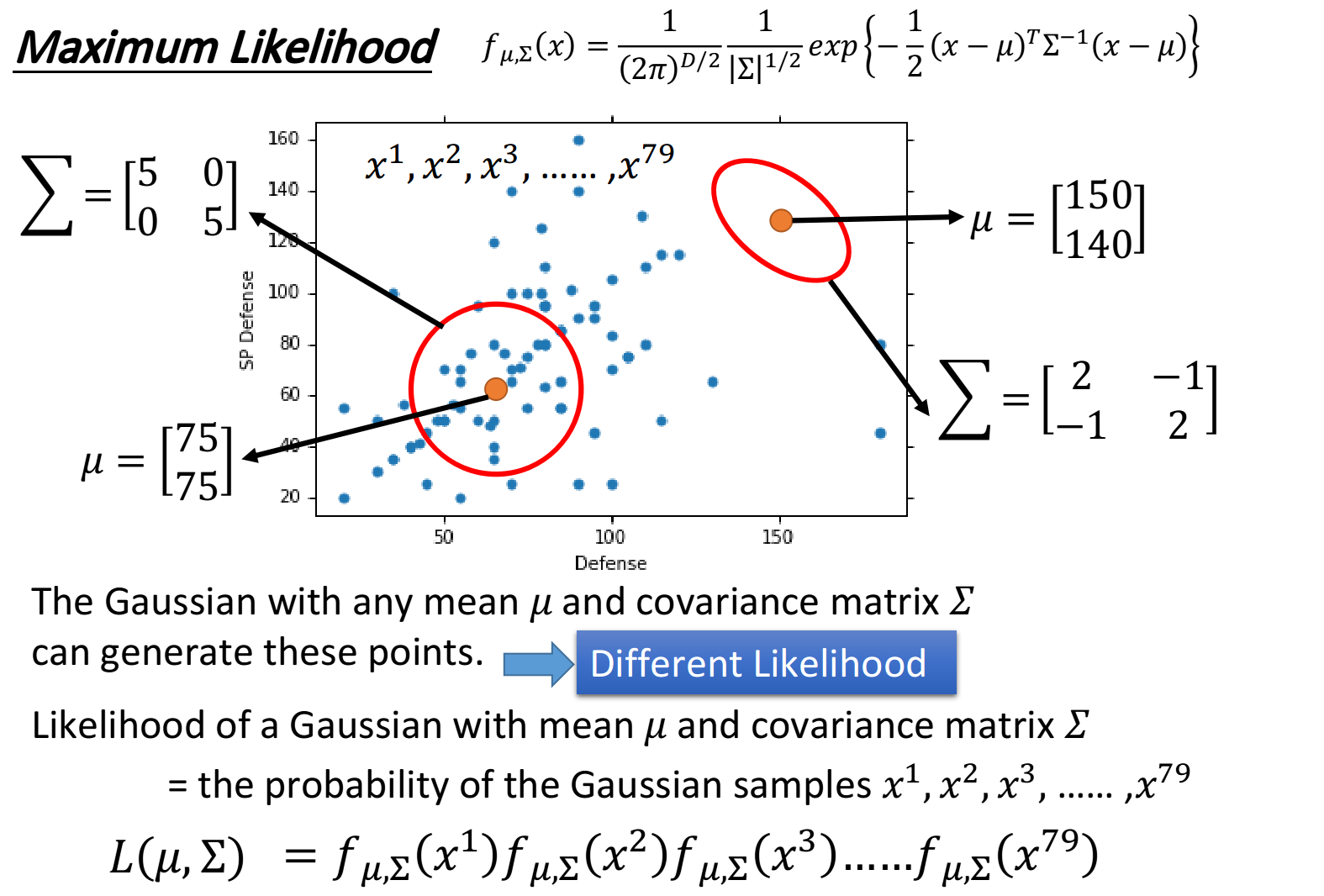
实际上任意一组
而极大似然函数
当然如果你不愿意去现场求微分的话,这也可以当做公式来记忆(
注:数学期望:
根据上述的公式和已有的79个点的数据,计算出class 1的两个参数:
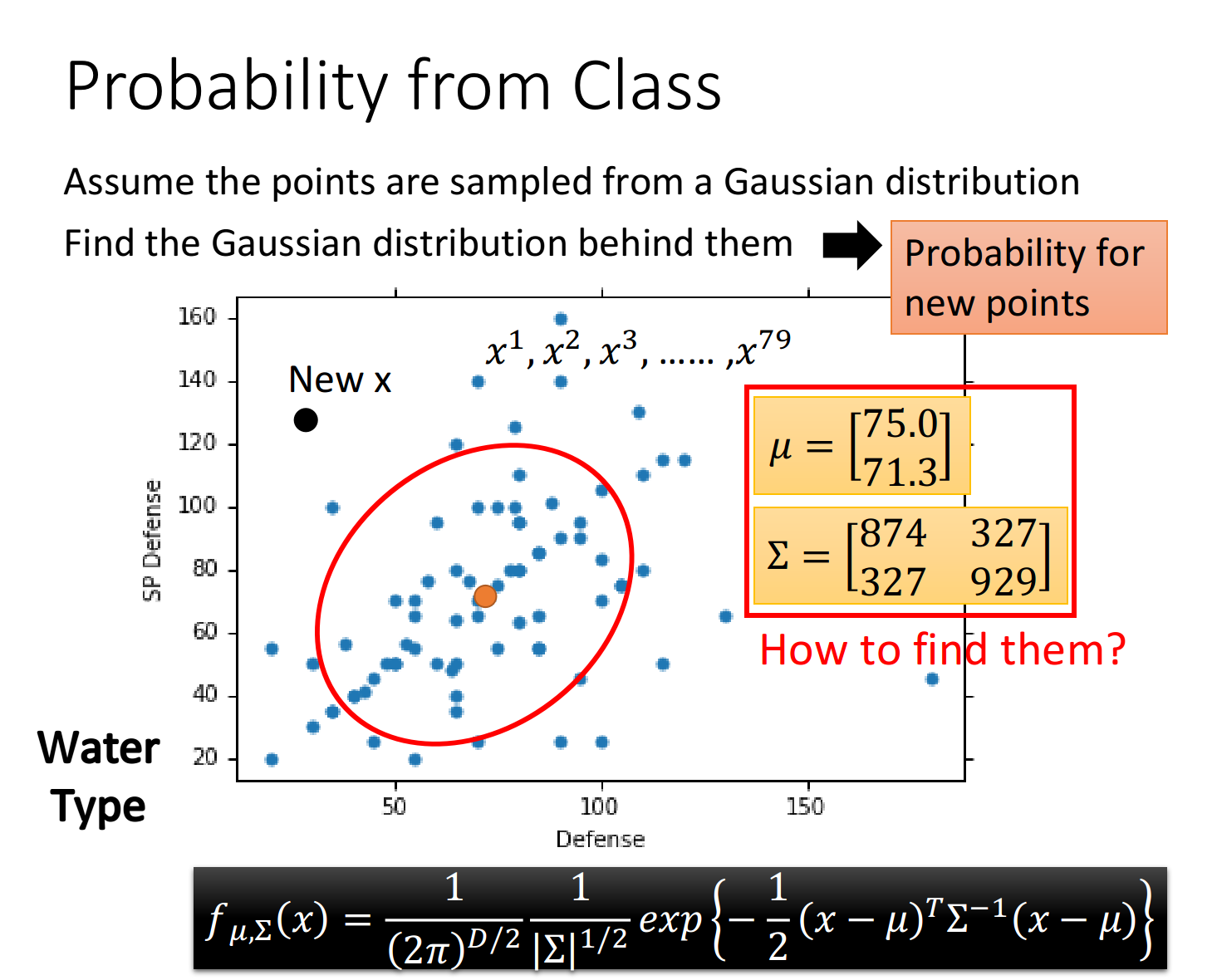
同理,我们用极大似然估计法在高斯函数上的公式计算出class 2的两个参数,得到的最终结果如下:
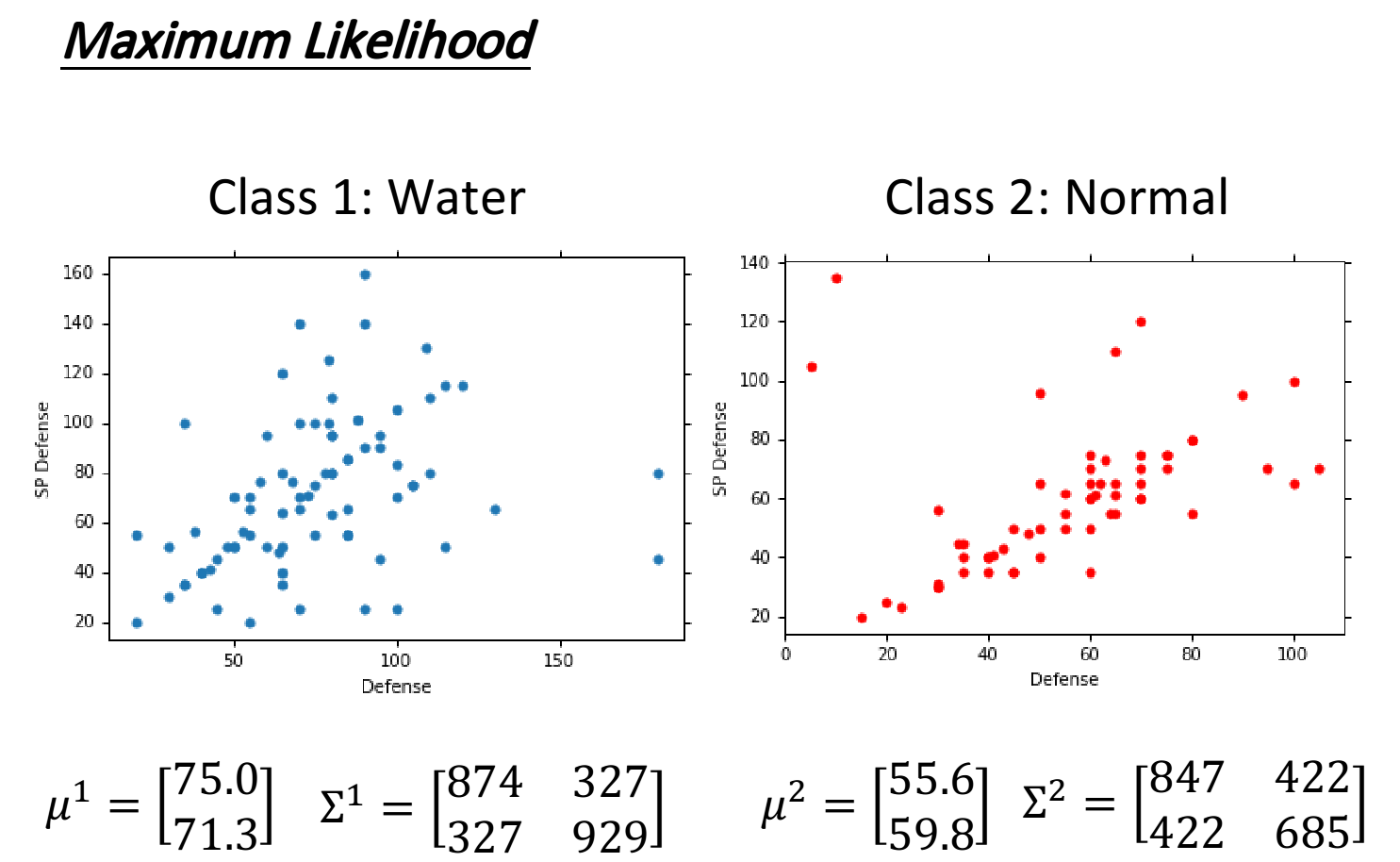
有了这些以后,我们可以得到
Do Classification!
已有的准备
现在我们已经有了以下数据和具体分布:

只要带入某一个input x,就可以通过这个式子计算出它是否是class 1了!
得到的结果
通过可视化得到的结果如下:
左上角的图中,横轴是Defense,纵轴是SP Defense,蓝色的点是水系的宝可梦的分布,红色的点是一般系的宝可梦的分布,对图中的每一个点都计算出它是class 1的概率
因为我们做的是分类问题,因此令几率>0.5的点为类别1,几率<0.5的点为类别2,也就是右上角的图中的红色和蓝色两块区域
再把testing data上得到的结果可视化出来,即右下角的图,发现分的不是太好,正确率才是47%
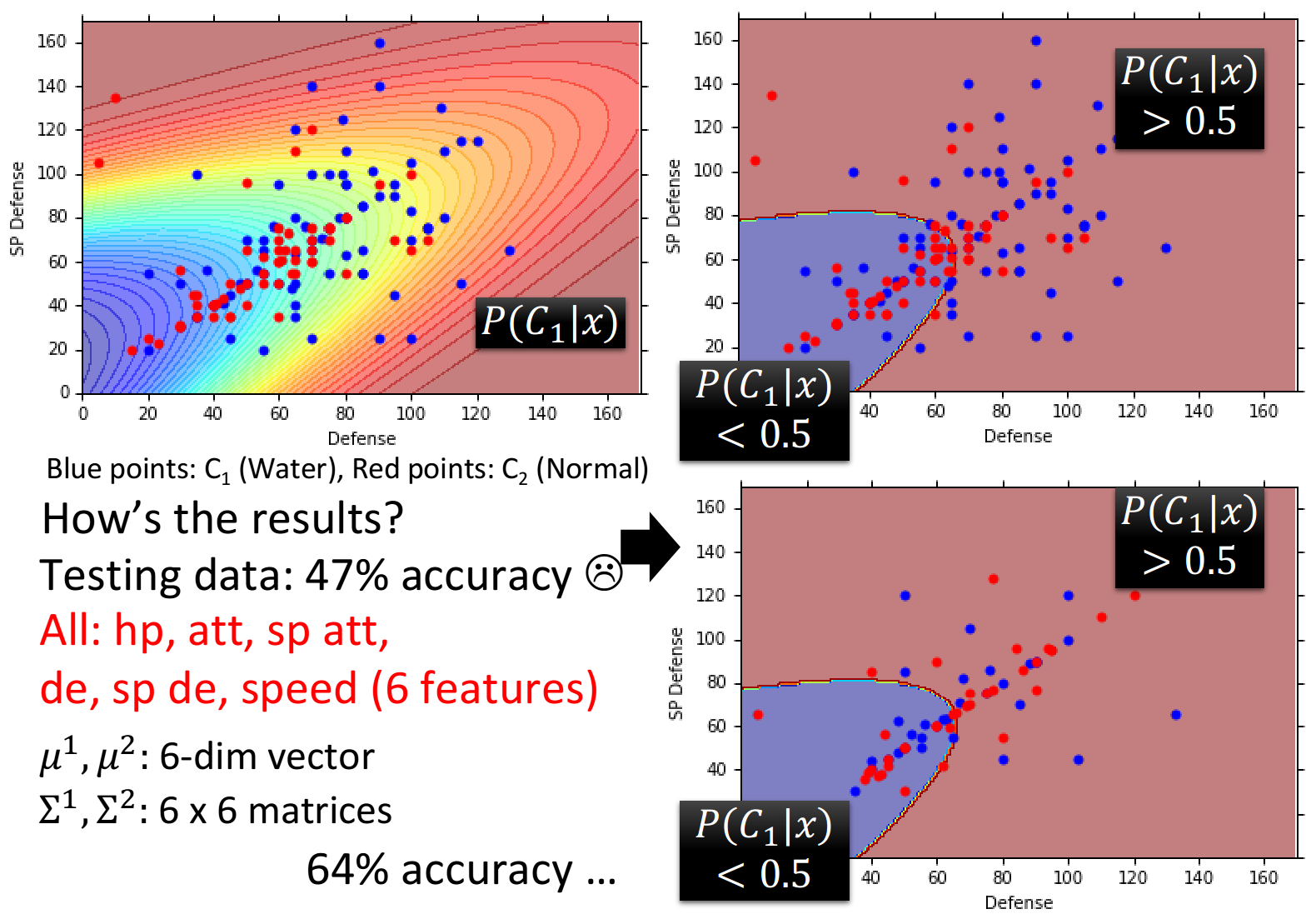
我们之前用的只是Defense和SP Defense这两个参数,在二维空间上得到的效果不太好,但实际上一开始就提到了宝可梦总共是有6个features的,也许在二维空间上它们是重叠在一起的,但是在六维空间上看它们也许会分得很好,每一个宝可梦都是六维空间中的一个点,于是我们的
Modifying Model
其实之前使用的model是不常见的,你是不会经常看到给每一个Gaussian都有自己的mean和covariance,比如我们的class 1用的是
其实variance是跟input的feature size的平方成正比的,所以当feature的数量很大的时候,
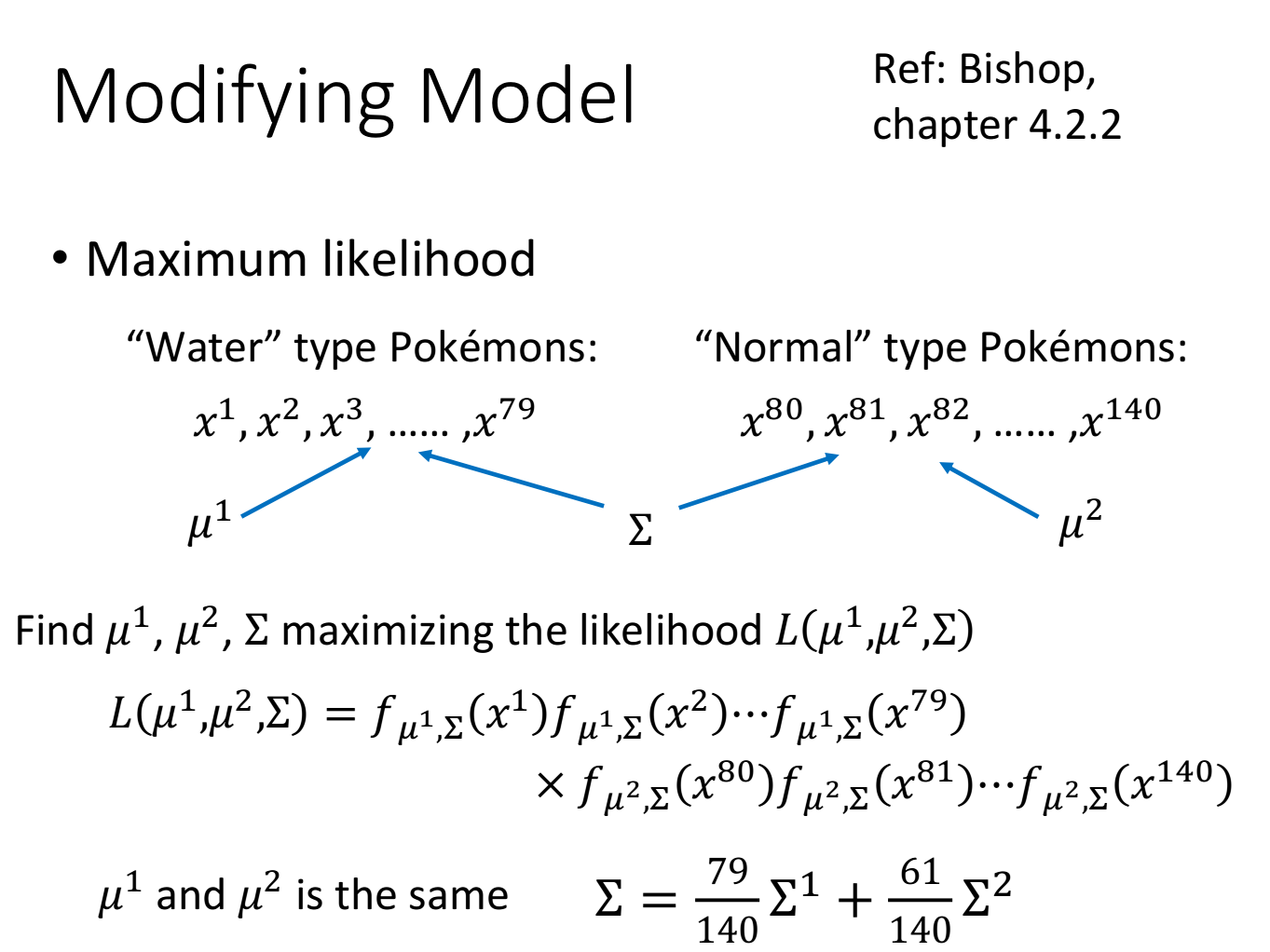
此时就把
再来看一下结果,你会发现,class 1和class 2在没有共用covariance matrix之前,它们的分界线是一条曲线;如果共用covariance matrix的话,它们之间的分界线就会变成一条直线,这样的model,我们也称之为linear model(尽管Gaussian不是linear的,但是它分两个class的boundary是linear)
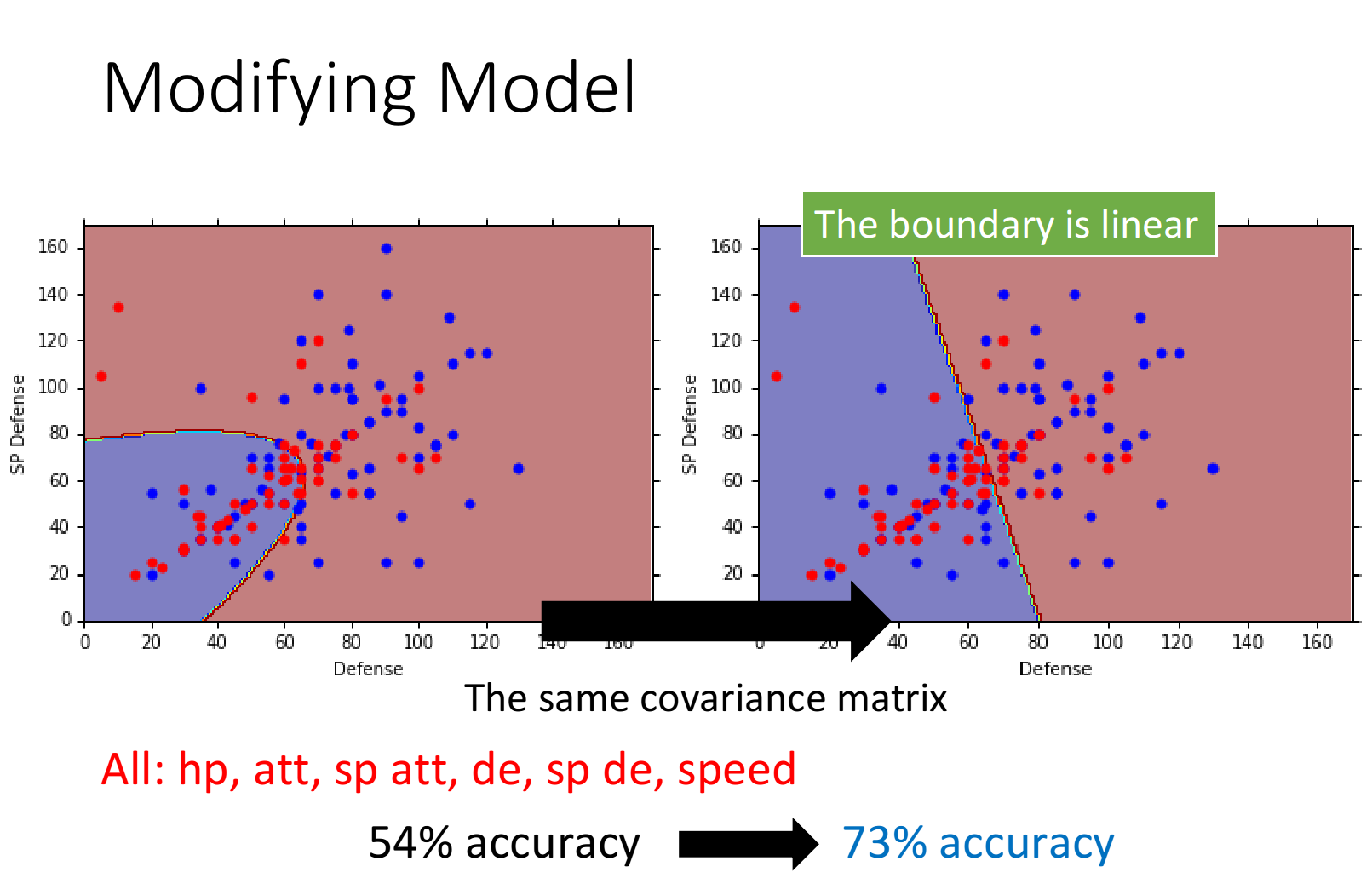
如果我们考虑所有的feature,并共用covariance的话,原来的54%的正确率就会变成73%,显然是有分对东西的,但是为什么会做到这样子,我们是很难分析的,因为这是在高维空间中发生的事情,我们很难知道boundary到底是怎么切的,但这就是machine learning它fancy的地方,人没有办法知道怎么做,但是machine可以帮我们做出来
Three Steps of classification
现在让我们来回顾一下做classification的三个步骤,实际上也就是做machine learning的三个步骤
Find a function set(model)
这些required probability
和probability distribution 就是model的参数,选择不同的Probability distribution(比如不同的分布函数,或者是不同参数的Gaussian distribution),就会得到不同的function,把这些不同参数的Gaussian distribution集合起来,就是一个model,如果不适用高斯函数而选择其他分布函数,就是一个新的model了 当这个posterior Probability
的话,就output class 1,反之就output class 2( ,因此没必要对class 2再去计算一遍) Goodness of function
对于Gaussian distribution这个model来说,我们要评价的是决定这个高斯函数形状的均值
和协方差 这两个参数的好坏,而极大似然函数 的输出值,就评价了这组参数的好坏 Find the best function
找到的那个最好的function,就是使
值最大的那组参数,实际上就是所有样本点的均值和协方差 这里上标i表示第i个点,这里x是一个features的vector,用下标来表示这个vector中的某个feature

Probability distribution
Why Gaussian distribution
你也许一直会有一个疑惑,为什么我们就要用Gaussian的model,而不选择别的分布函数,其实这里只是拿高斯分布函数举一个例子而已,你当然可以选择自己喜欢的Probability distribution概率分布函数,如果你选择的是简单的分布函数(参数比较少),那你的bias就大,variance就小;如果你选择复杂的分布函数,那你的bias就小,variance就大,那你就可以用data set来判断一下,用什么样的Probability distribution作为model是比较好的
Naive Bayes Classifier(朴素贝叶斯分类法)
我们可以考虑这样一件事情,假设
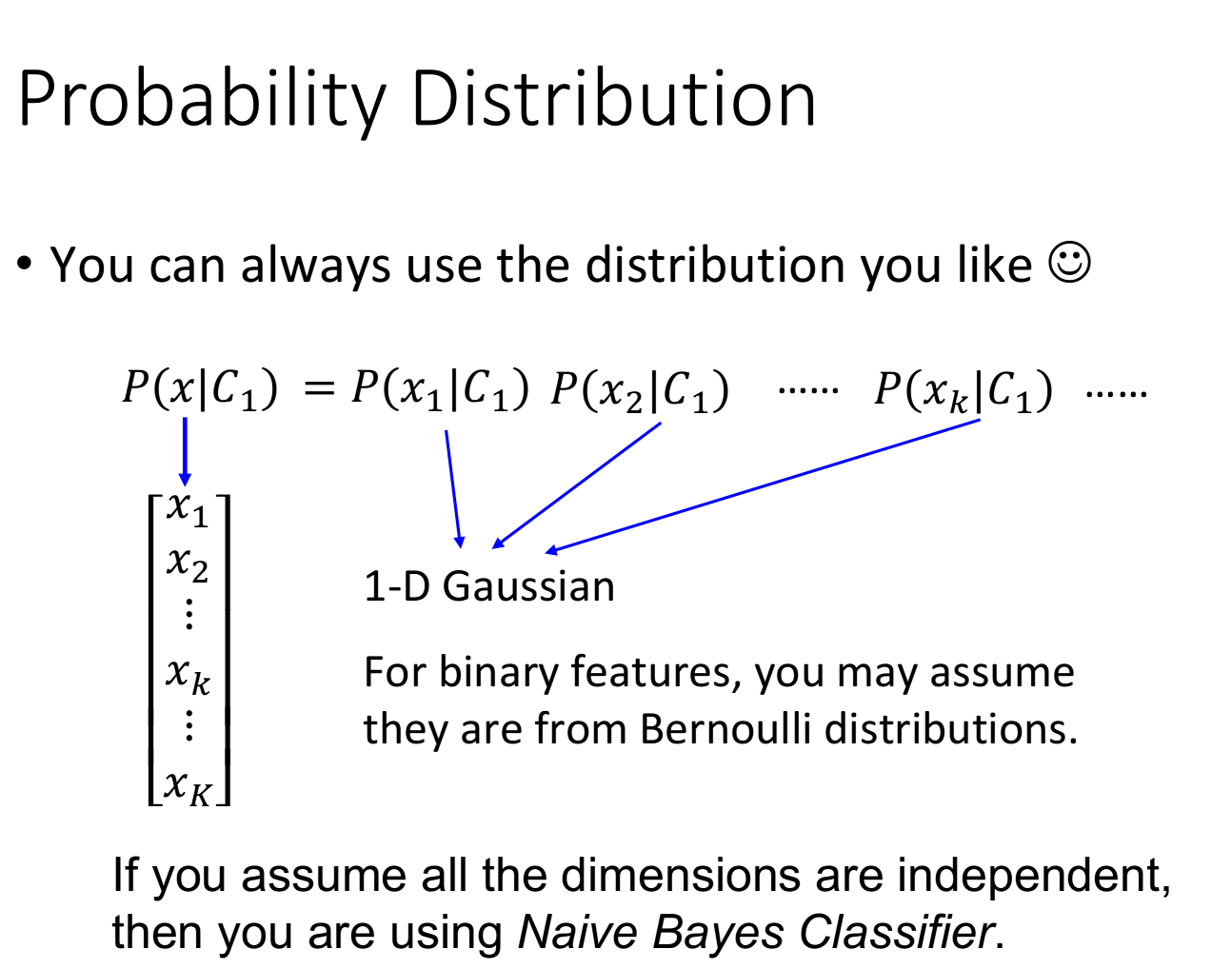
这里每一个dimension的分布函数都是一维的Gaussian distribution,如果这样假设的话,等于是说,原来那多维度的Gaussian,它的covariance matrix变成是diagonal(对角的),在不是对角线的地方,值都是0,这样就可以更加减少需要的参数量,就可以得到一个更简单的model
我们把上述这种方法叫做==Naive Bayes Classifier(朴素贝叶斯分类法)==,如果真的明确了所有的feature之间是相互独立的,是不相关的,使用朴素贝叶斯分类法的performance是会很好的,如果这个假设是不成立的,那么Naive bayes classfier的bias就会很大,它就不是一个好的classifier(朴素贝叶斯分类法本质就是减少参数)
当然这个例子里如果使用这样的model,得到的结果也不理想,因为各种feature之间的covariance还是必要的,比如战斗力和防御力它们之间是正相关的,covariance不能等于0
总之,寻找model总的原则是,尽量减少不必要的参数,但是必然的参数绝对不能少
那怎么去选择分布函数呢?有很多时候凭直觉就可以看出来,比如宝可梦有某个feature是binary的,它代表的是:是或不是,这个时候就不太可能是高斯分布了,而很有可能是伯努利分布(两点分布)
Analysis Posterior Probability
接下来我们来分析一下这个后置概率的表达式,会发现一些有趣的现象
表达式上下同除以分子,得到
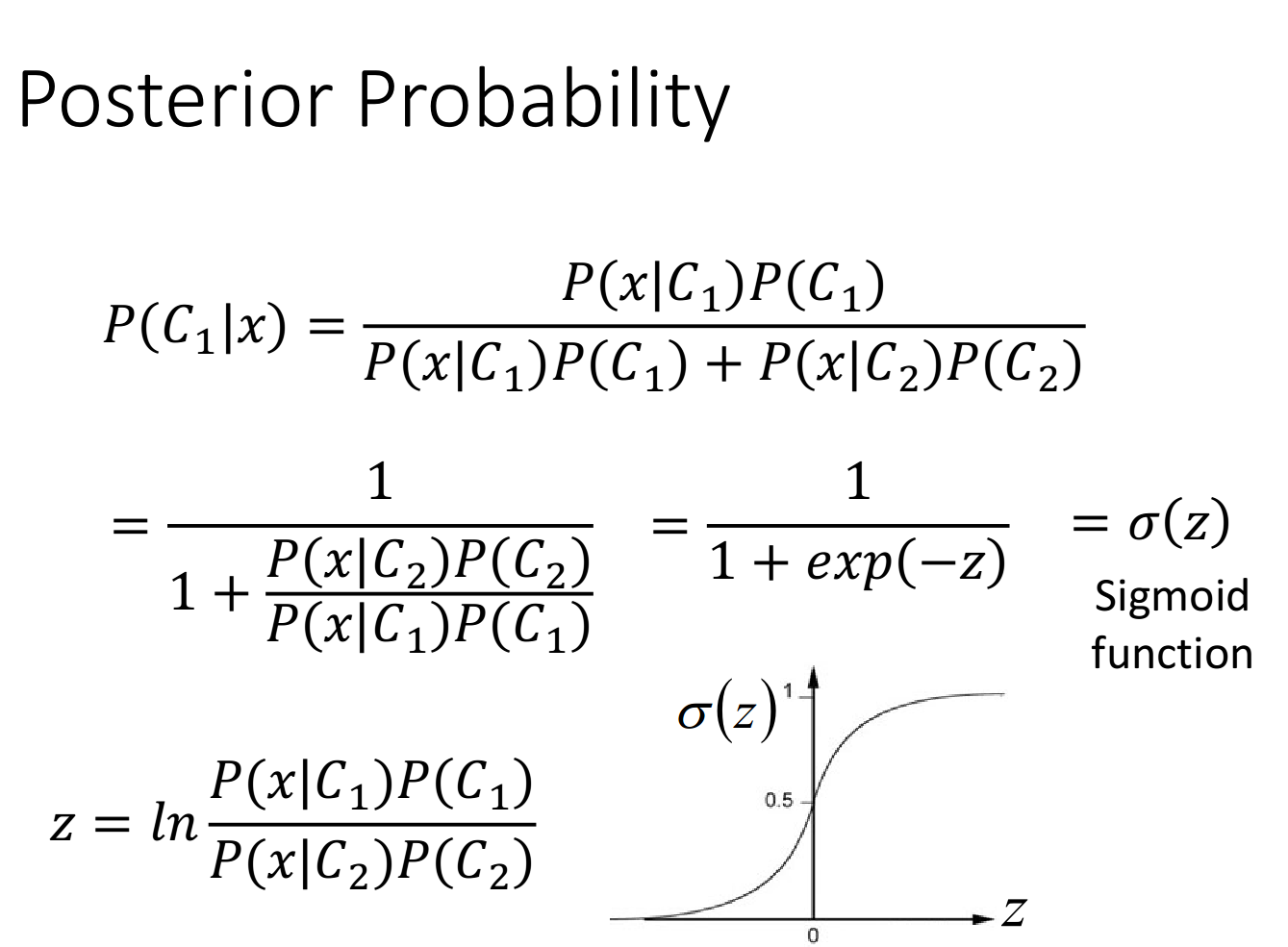
这个S函数是已知逻辑函数,现在我们来推导一下z真正的样子,推导过程如下:
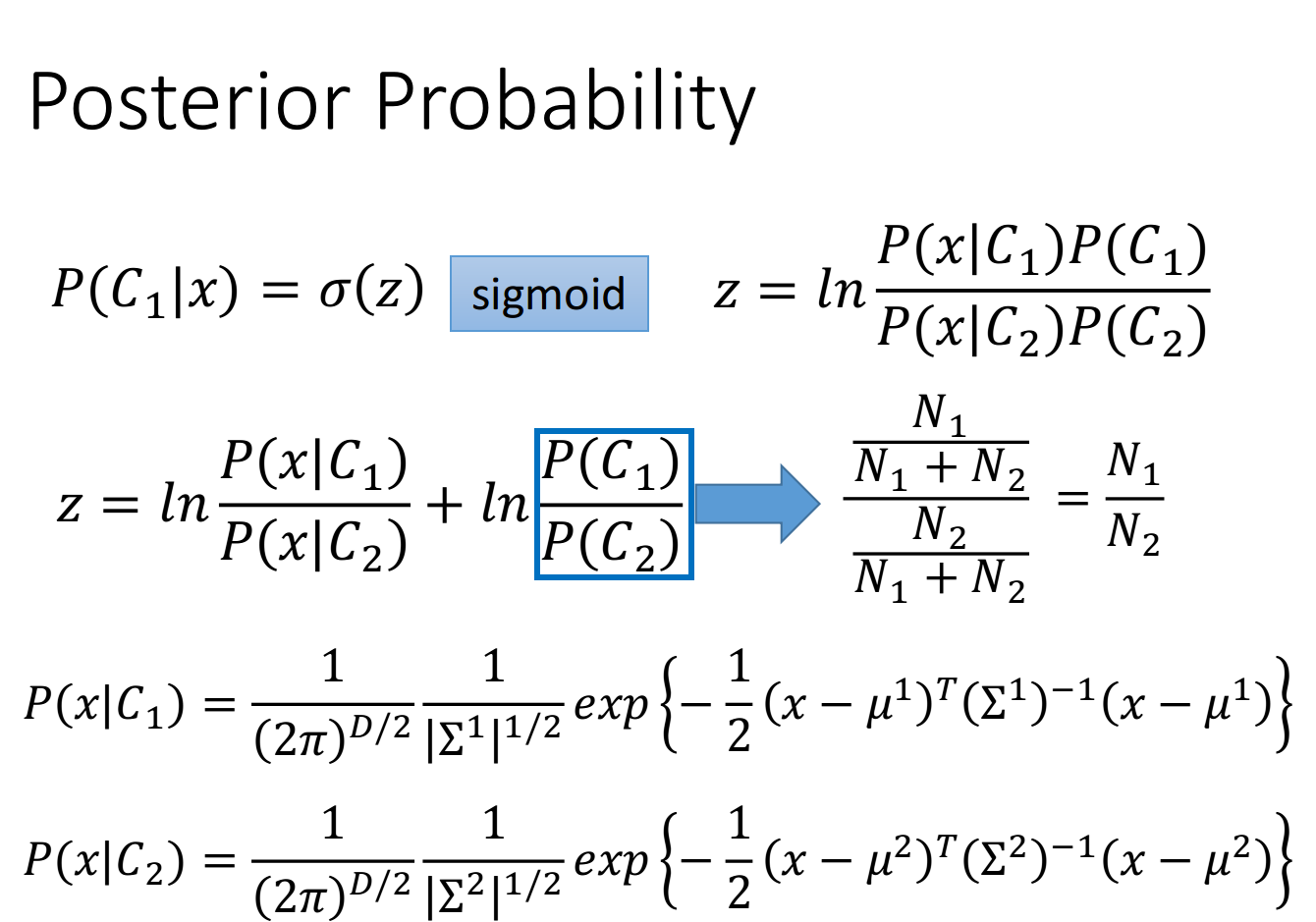
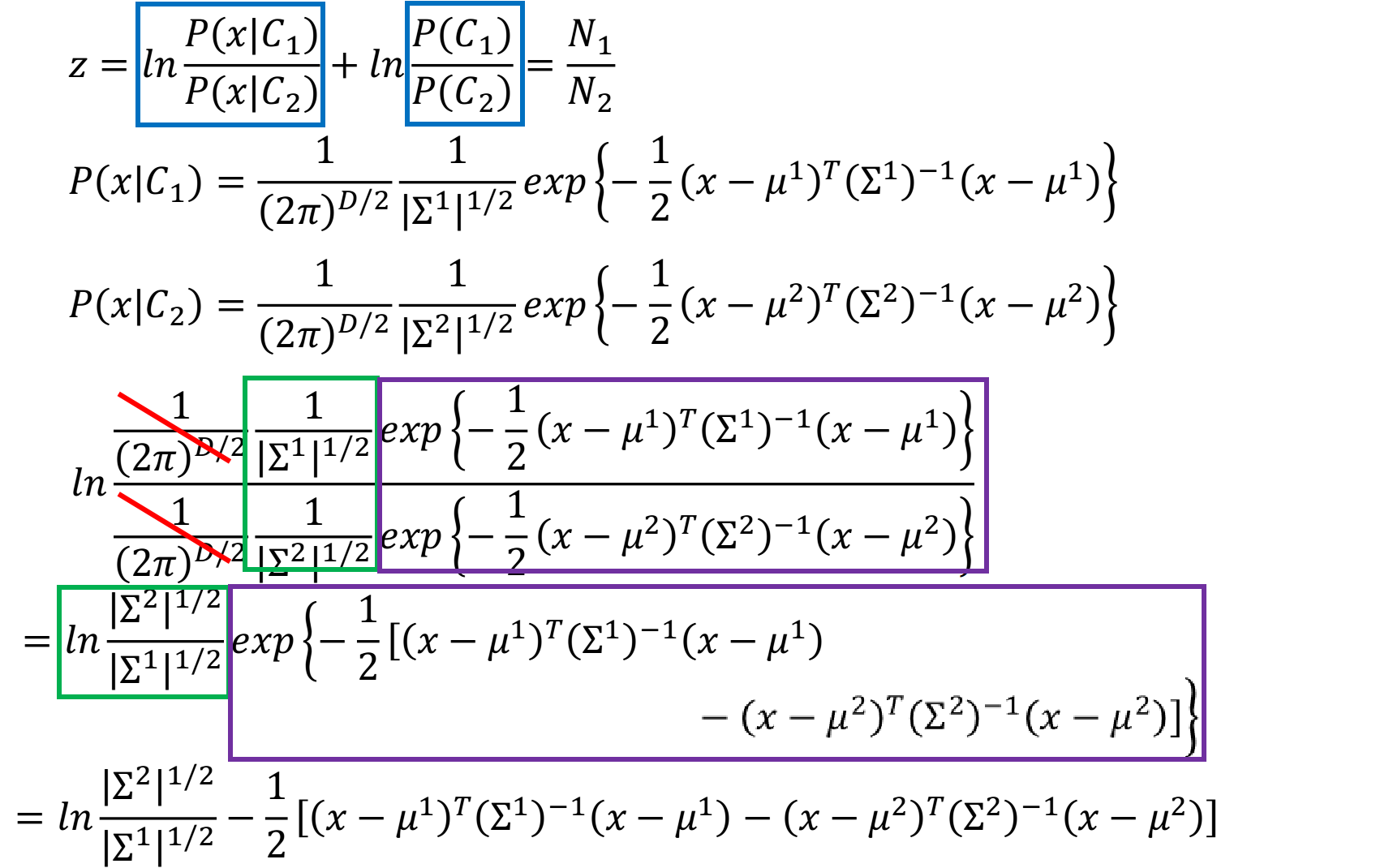
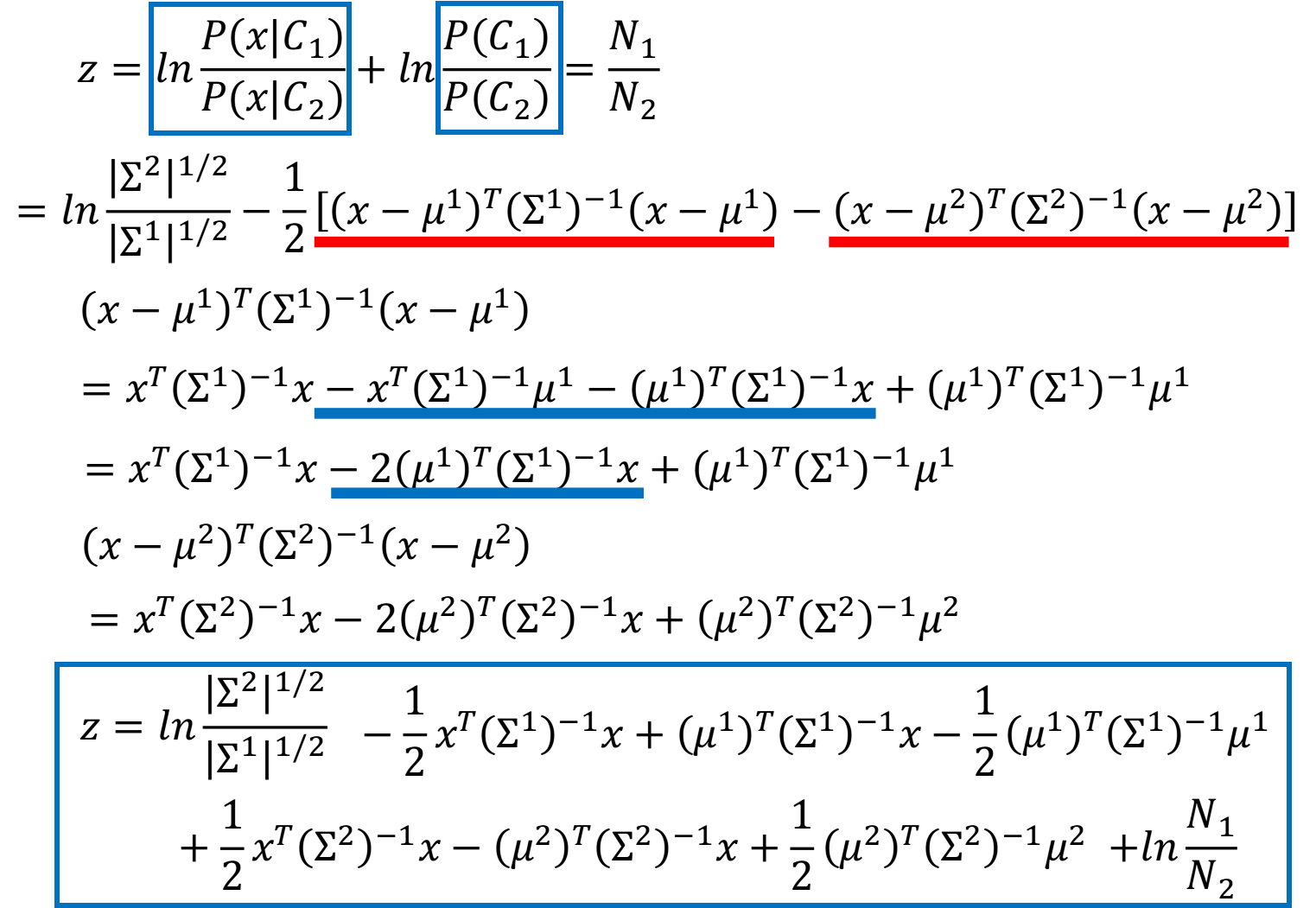
上面的推导过程可能比较复杂,但是得到的最终结果还是比较好的:(当
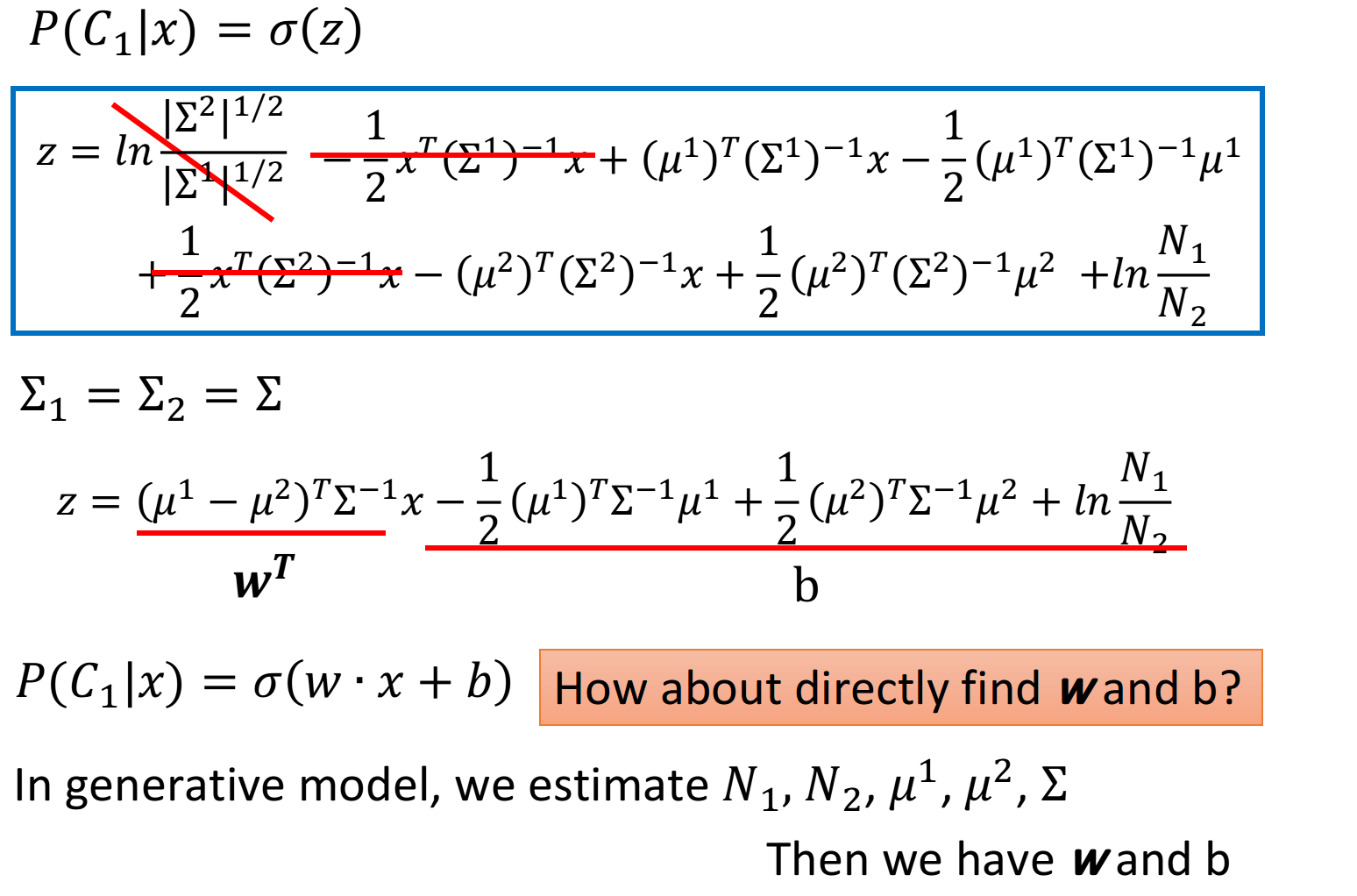
==
那在Generative model里面,我们做的事情是,我们用某些方法去找出
所以我们能不能直接把w和b找出来呢?这是下一章节的内容
