Unsupervised Learning: PCA(Ⅰ)
本文将主要介绍PCA算法的数学推导过程
上一篇文章提到,PCA算法认为降维就是一个简单的linear function,它的input x和output z之间是linear transform,即
PCA for 1-D
为了简化问题,这里我们假设z是1维的vector,也就是把x投影到一维空间,此时w是一个row vector
那我们到底要找什么样的
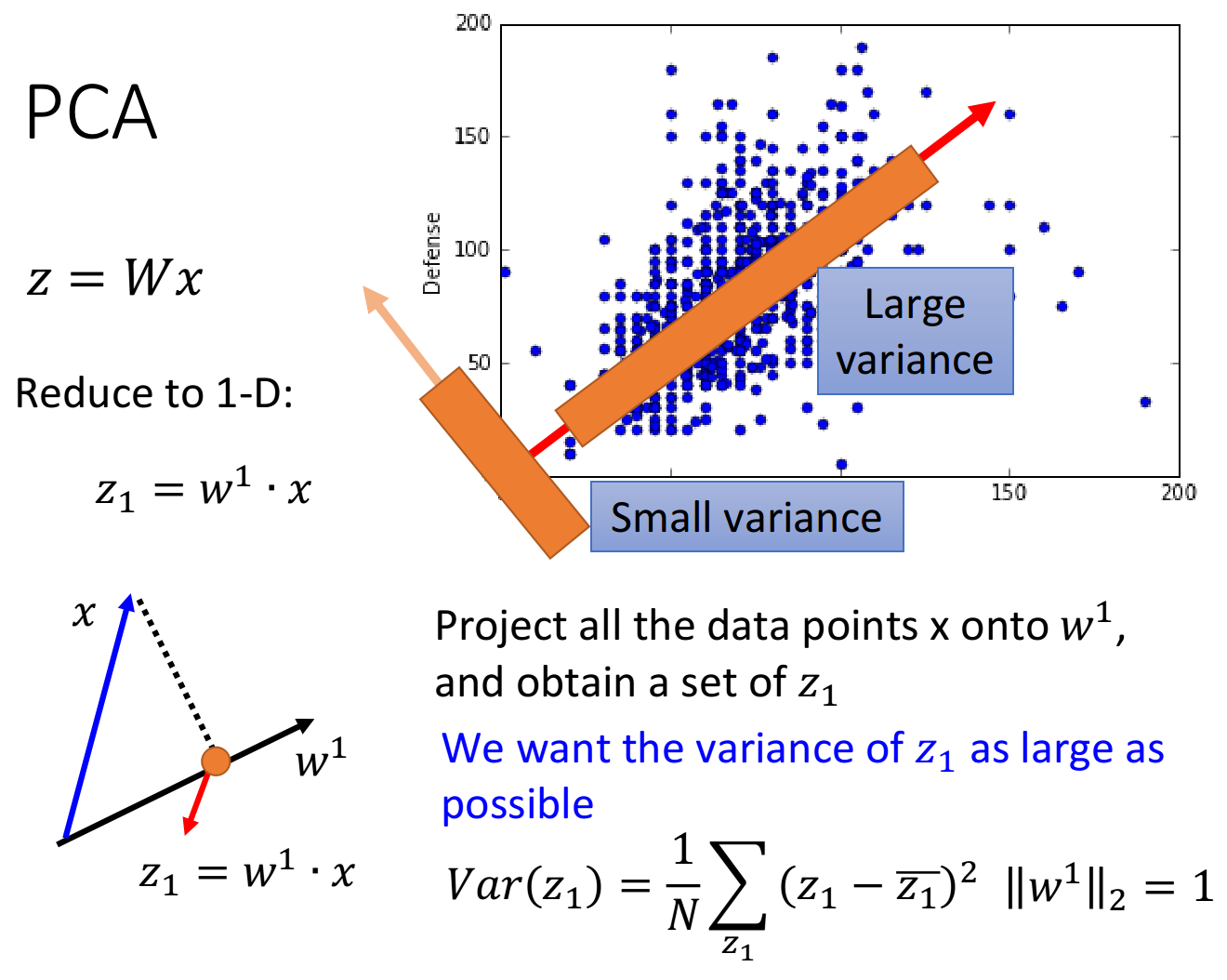
假设我们现在已有的宝可梦样本点分布如下,横坐标代表宝可梦的攻击力,纵坐标代表防御力,我们的任务是把这个二维分布投影到一维空间上
我们希望选这样一个
我们希望找一个projection的方向,它可以让projection后的variance越大越好
我们不希望projection使这些data point通通挤在一起,导致点与点之间的奇异度消失
其中,variance的计算公式:
, 是 的平均值
下图给出了所有样本点在两个不同的方向上投影之后的variance比较情况
PCA for n-D
当然我们不可能只投影到一维空间,我们还可以投影到更高维的空间
对
,表示 在 方向上的投影 ,表示 在 方向上的投影 - ...

Lagrange multiplier
求解PCA,实际上已经有现成的函数可以调用,此外你也可以把PCA描述成neural network,然后用gradient descent的方法来求解,这里主要介绍用拉格朗日乘数法(Lagrange multiplier)求解PCA的数学推导过程
注:
calculate
目标:maximize $(w^1)^TSw^1
首先计算出
: 然后计算maximize的对象
: 其中
当然这里想要求
的最大值,还要加上 的约束条件,否则 可以取无穷大 令
,它是: - 对称的(symmetric)
- 半正定的(positive-semidefine)
- 所有特征值(eigenvalues)非负的(non-negative)
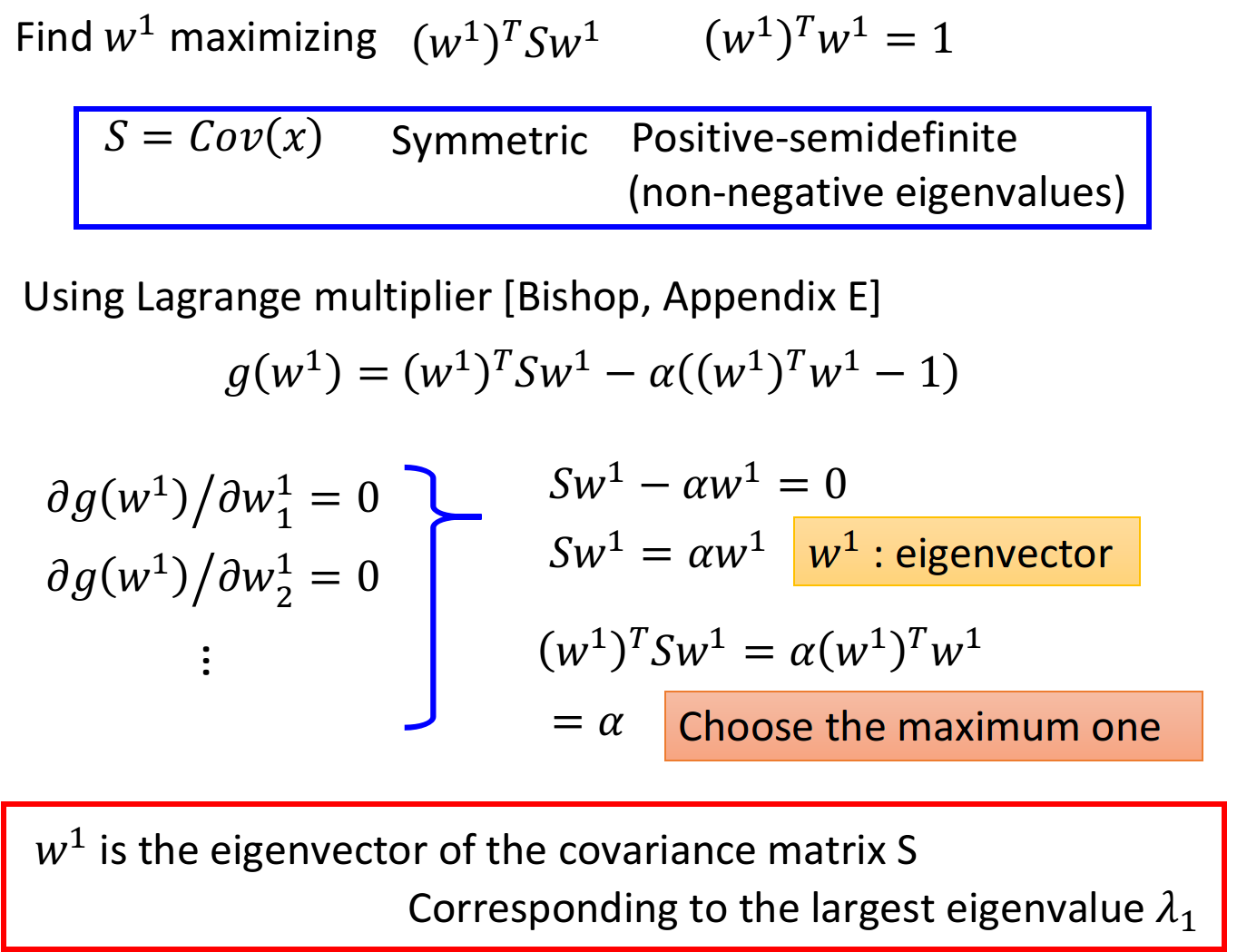
使用拉格朗日乘数法,利用目标和约束条件构造函数:
对
这个vector里的每一个element做偏微分: 整理上述推导式,可以得到:
其中,
是S的特征向量(eigenvector) 注意到满足
的特征向量 有很多,我们要找的是可以maximize 的那一个,于是利用上一个式子: 此时maximize
就变成了maximize ,也就是当 的特征值 最大时对应的那个特征向量 就是我们要找的目标 结论:
是 这个matrix中的特征向量,对应最大的特征值
calculate
在推导
目标:maximize
结论:
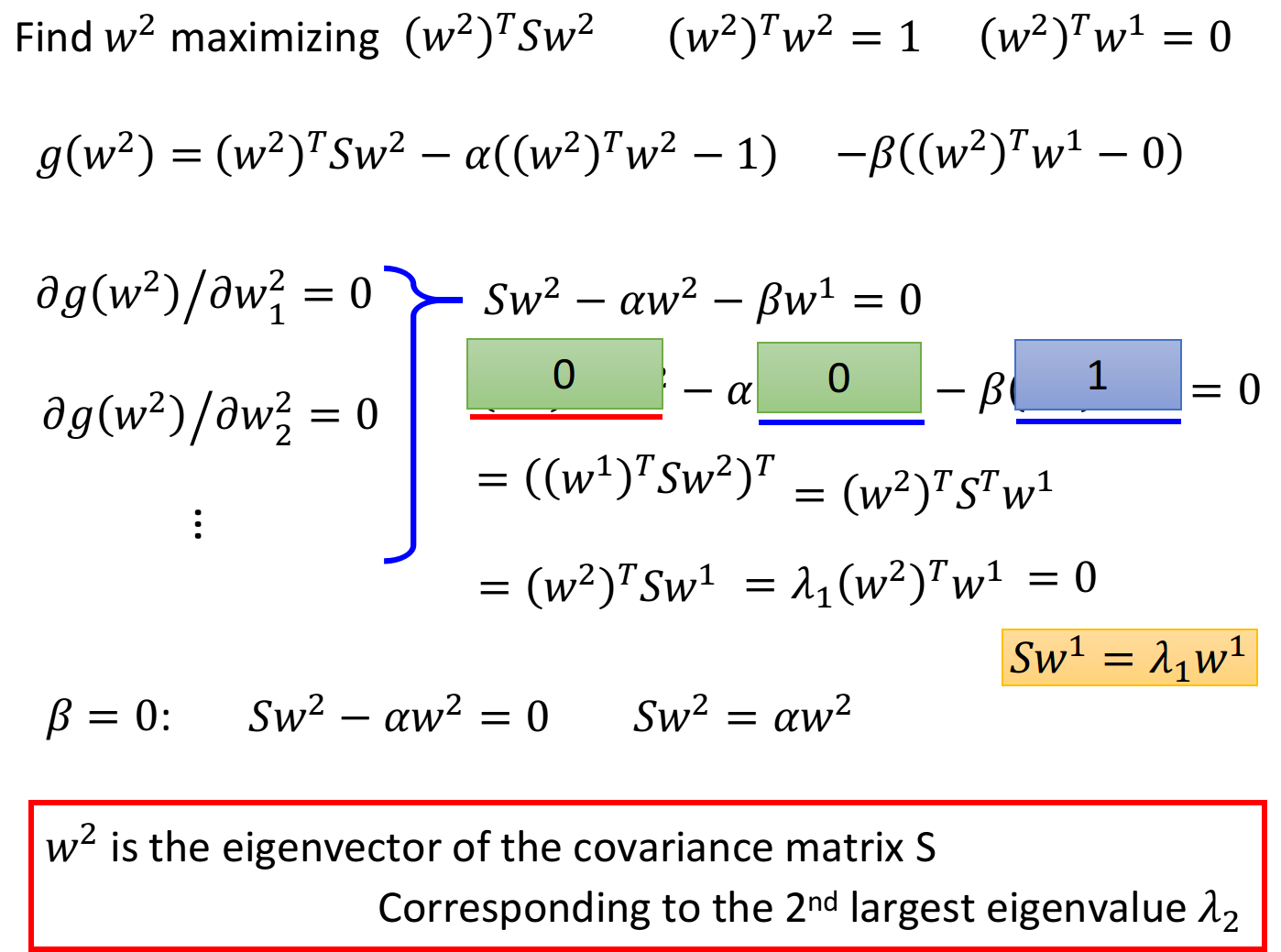
同样是用拉格朗日乘数法求解,先写一个关于
的function,包含要maximize的对象,以及两个约束条件 对
的每个element做偏微分: 整理后得到:
上式两侧同乘
,得到: 其中
, 而由于
是vector×matrix×vector=scalar,因此在外面套一个transpose不会改变其值,因此该部分可以转化为: 注:S是symmetric的,因此
我们已经知道
满足 ,代入上式: 因此有
, , ,又根据 可以推得
此时
就转变成了 ,即 由于
是symmetric的,因此在不与 冲突的情况下,这里 选取第二大的特征值 时,可以使 最大 结论:
也是 这个matrix中的特征向量,对应第二大的特征值
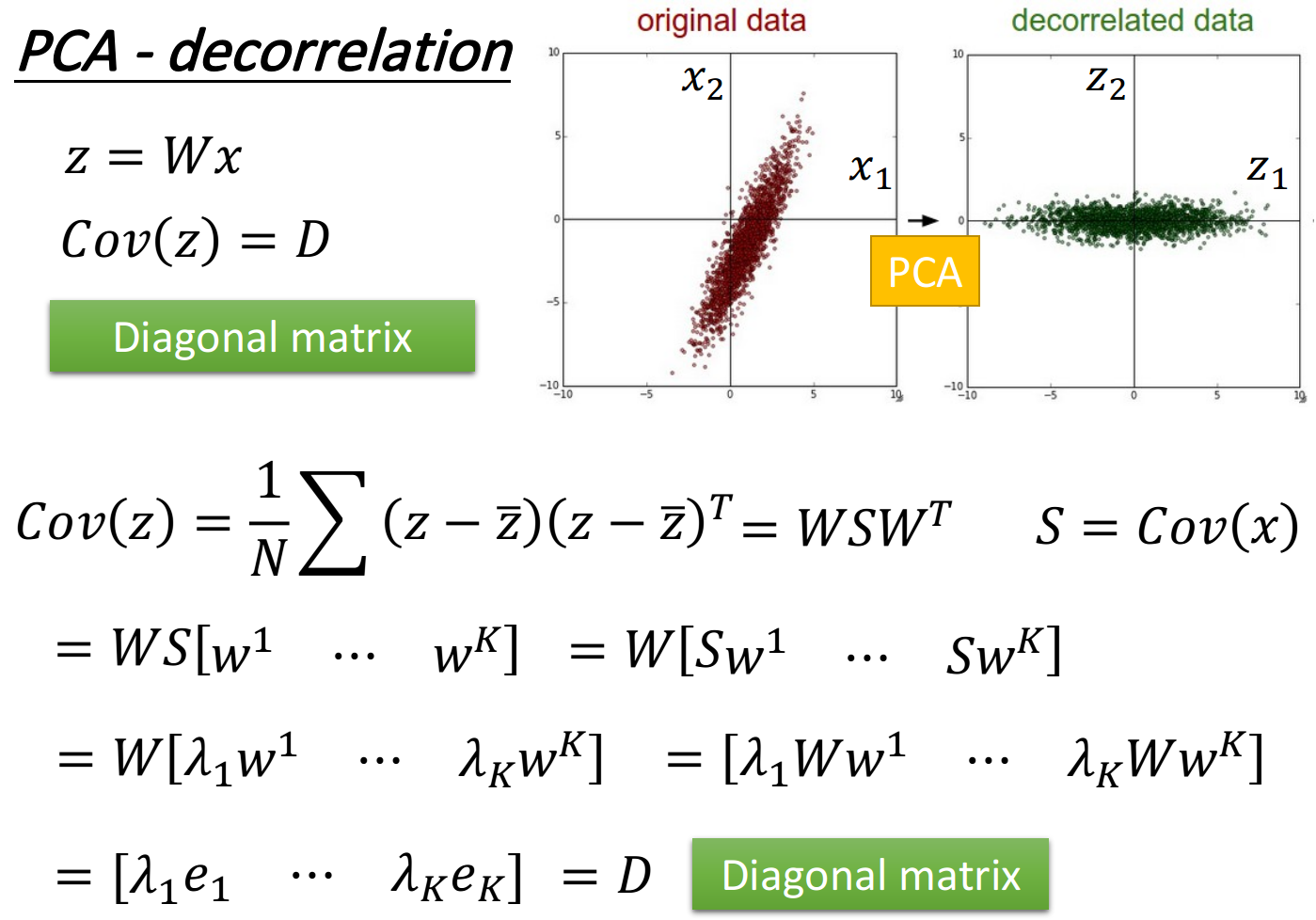
PCA-decorrelation
神奇之处在于
PCA可以让不同dimension之间的covariance变为0,即不同new feature之间是没有correlation的,这样做的好处是,减少feature之间的联系从而减少model所需的参数量
如果你把原来的input data通过PCA之后再给其他model使用,那这些model就可以使用简单的形式,而无需考虑不同dimension之间类似
本文主要介绍的是PCA的数学推导,如果你理解起来有点困难,那下一篇文章将会从另一个角度解释PCA算法的原理~
