正则化
原文链接
- https://developers.google.com/machine-learning/crash-course/regularization-for-simplicity/l2-regularization?hl=zh-cn
- https://developers.google.com/machine-learning/crash-course/regularization-for-simplicity/lambda?hl=zh-cn
- https://developers.google.com/machine-learning/crash-course/regularization-for-sparsity/l1-regularization?hl=zh-cn
简单性
请考虑以下泛化曲线,该曲线显示的是训练集和验证集相对于训练迭代次数的损失。
图 1. 训练集和验证集的损失。
图 1 显示了一个模型,其中训练损失逐渐减少,但验证损失最终增加。换言之,该泛化曲线显示模型与训练集中的数据过拟合。根据奥卡姆的内在结构,或许我们可以通过降低复杂模型的复杂度来防止过拟合,这种原则称为正则化。
换言之,不应只是以最小化损失(经验风险最小化)为目标:
而是以最小化损失和复杂度为目标,这称为结构风险最小化:
现在,我们的训练优化算法是一个由两项内容组成的函数:一个是损失项,用于衡量模型与数据的拟合度,另一个是正则化项,用于衡量模型复杂度。
机器学习速成课程重点介绍了两种衡量模型复杂度的常见方式(两者在一定程度上相关):
- 将模型复杂度作为模型中所有特征的权重的函数。
- 将模型复杂度作为具有非零权重的特征总数的函数。(后面的一个单元介绍了此方法。)
如果模型复杂度是权重的函数,则特征权重的绝对值越高,对模型复杂度的贡献就越大。
我们可以使用
在此公式中,接近于 0 的权重对模型复杂度几乎没有影响,而离群值权重则会产生巨大的影响。
例如,某个线性模型具有以下权重:
但是,
Lambda
模型开发者通过以下方式来调整正则化项的整体影响:用正则化项的值乘以名为 (也称为正则化率)的标量。也就是说,模型开发者旨在执行以下操作:
执行
- 使权重值接近于 0(但并非正好为 0)
- 使权重的平均值接近 0,并且呈正态(钟形或高斯)分布。
增加 lambda 值会增强正则化效果。例如,lambda 值较高的权重直方图可能如图 2 所示。
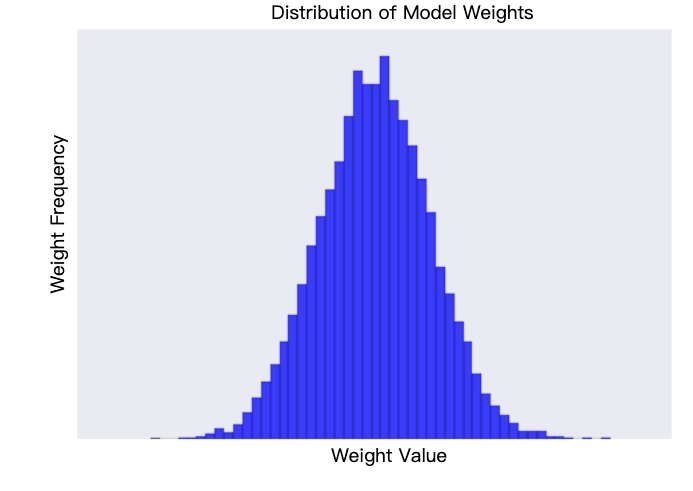
图 2. 权重直方图。
降低 lambda 的值往往会生成一个更扁平的直方图,如图 3 所示。
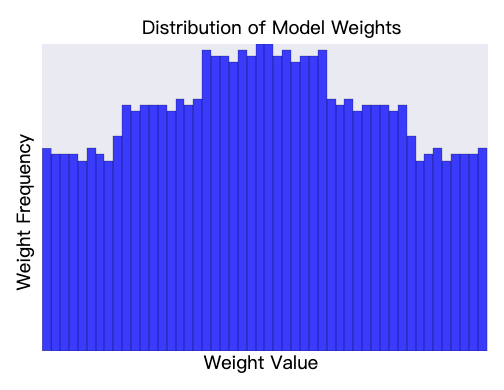
图 3. 由较低的 lambda 值生成的权重直方图。
选择 lambda 值时,目标是在简单性和训练数据拟合之间取得适当的平衡:
如果 lambda 值过高,则模型会非常简单,但是您将面临数据欠拟合的风险。模型将无法从训练数据中获得足够的信息来做出有用的预测。
如果 lambda 值过低,则模型会比较复杂,并且您将面临数据过拟合的风险。您的模型将了解过多训练数据的特殊性,无法泛化到新数据。
理想的 lambda 值生成的模型可以很好地泛化到以前未见过的新数据。遗憾的是,理想的 lambda 值取决于数据,因此您需要手动或自动进行一些 调整。
点击加号图标即可了解
学习速率与 lambda 之间存在密切关联。
早停法是指在模型完全收敛之前结束训练。在实践中,以在线(连续)方式进行训练时,我们通常最终会获得一定程度的隐式早停法。也就是说,一些新趋势的数据尚不足以收敛。
如上所述,改变正则化参数的影响可能与学习速率或迭代次数变化的影响相混淆。一种有用的做法(在对固定批次的数据进行训练时)是进行足够多的迭代,这样提前停止不会产生任何影响。
稀疏性
稀疏矢量通常包含许多维度。创建特征组合会导致包含更多维度。鉴于此类高维度特征向量,模型大小可能会变得庞大,并且需要大量的 RAM。
在高维度稀疏矢量中,最好尽可能使权重正好降至 0。正好为 0 的权重基本上会从模型中移除相应特征。将特征设为 0 可以节省 RAM,并可以减少模型中的噪声。
例如,假设某个住房数据集不仅涵盖加利福尼亚州,而且涵盖全球。如果按分钟(每度 60 分钟)对全球纬度进行分桶,则会在稀疏编码中获得大约 10,000 个维度;如果按分钟对全球经度进行分桶,则会产生大约 20,000 个维度。这两个特征的特征组合会产生大约 2 亿个维度。这 2 亿个维度中的许多维度都表示居住地非常有限的区域(例如海洋中部),很难利用这些数据进行有效泛化。如果代付存储这些不需要的维度的 RAM 开销就太不明智了。因此,最好是将无意义维度的权重降至正好 0,从而避免在推断时为这些模型系数的存储成本付费。
我们或许能够通过添加适当选择的正则化项,将此想法编码为训练时解决的优化问题。
另一种方法是尝试创建一个正则化项,减少模型中非零系数值的数量。只有在模型能够与数据拟合时,增加此计数才有意义。遗憾的是,虽然这种基于计数的方法看起来很有吸引力,但它会将我们的凸优化问题转变为非凸优化问题。因此,L0 正则化这种想法在实践中并不现实。
不过,
会降低 会降低 。
因此,
的导数为 的导数为 (一个常数,其值与权重无关)。
您可以将
您可以将
请注意,该说明适用于一维模型。
点击下面的“播放”按钮 (),比较

